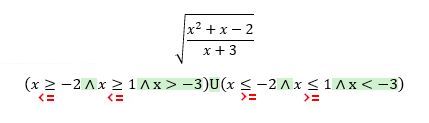Čau, chtěl bych se prosim vás zeptat v čem dělam chybu. Už jsem trochu vyšel ze cviku a stale nemužu najit chybu.
0x
Obrázek vložen přímo.
Jmenovatel nesmí být nula: x ≠ -3
Výraz pod odmocninou nesmí být záporný. Zde asi děláš chybu. Když násobíš tu nerovnici (x+3), tak se ti to rozpadne na 2 případy podle toho, je-li výraz (x+3) kladný (neboli x>-3), znaménko nerovnice se nemění, jestli je ale (x+3) záporné (tedy x<-3), tak se znaménko nerovnice otočí (neboli x2 + x - 2
doplněno 09.01.17 08:13:
Poradna má dlouhodobé problémy se znaky "větší/menší než".![]()
... neboli x2 + x - 2 menší než x + 3, pro x menší než -3.
doplněno 09.01.17 11:31:
Koukám, co jsem to napsal za blbost ![]()
Mělo být: ... neboli x2 + x - 2 menší než NULA, pro x menší než -3 (protože 0.(x+3) = 0 a ne (x+3) ) ![]()
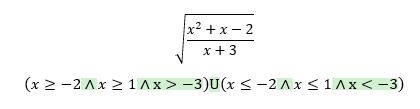
Já bych trochu nesouhlasil. To že x musí být různé od -3 o tom žádná řeč. Ovšem že odmocnina nesmí být záporná? I iracionální řešení je řešení, pokud není podmínka, že řešení musí být v oboru racionálních čísel.
Podle výsledku zjevně hledají def.obor v rámci reálných čísel.![]()
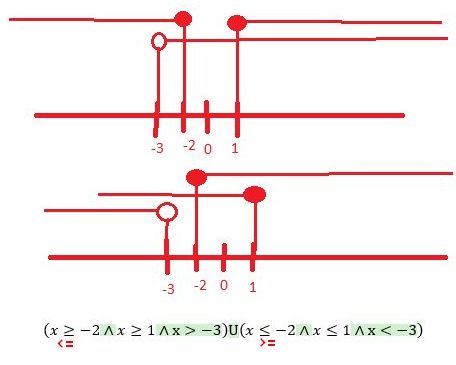
Je tam také vidět ten rozpad na ty 2 případy (větší/menší než -3).
Pro tazatele: ten zápis jejich výsledku jde ještě výrazně zjednodušit. Nakresli si to na ose. V tomto tvaru to mají asi schválně proto, aby bylo vidět, jak se na řešení přijde.
Tedˇ jsem moc nepochopil co se tady řeši :D . Stači napsat kde jsem udělal chybu, protože ja ji tam stále nevidím.
doplněno 09.01.17 11:50:
Jinak ano, jedna se o realné čísla.
Aha, já se až teď pořádně podíval na ten výsledek a pochopil, že je tvůj a je v něm dost chyb ![]()
Máš tam špatně znaménka (viz moje červená).
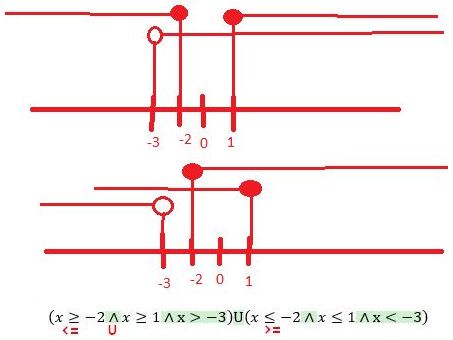
První dvojice v každé závorce nemá být "a zároveň", ale "sjednoceno/nebo".
Po zjednodušení prvního intervalu ti vyjde: (-3;-2] U [1;inf)
Druhá závorka tvojeho výsledku dá prázdnou množinu (čísla musí být mezi -2 a 1 a zároveň menší než -3).
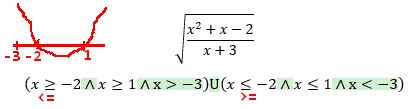
Podle toho vašeho to teš nevychází. To navrchu je funkce to pod tím jsem dělal ja, prosím vás potřeboval bych to co nejdřive ![]() .
.
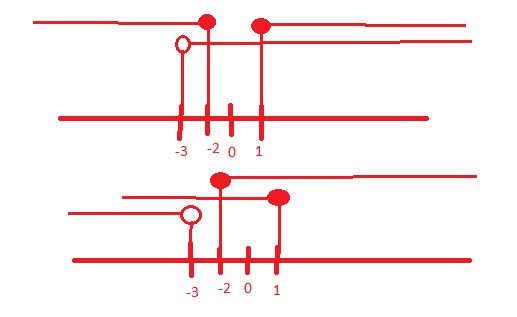
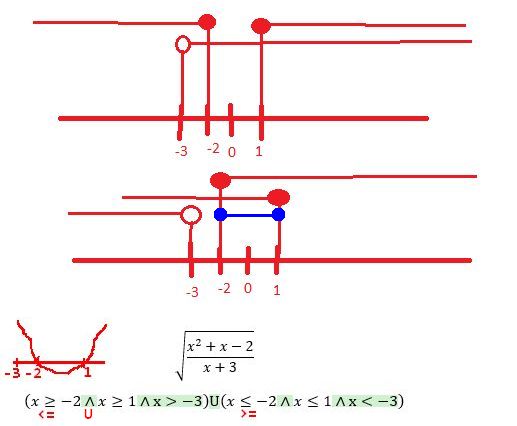
Napsal jsem to blbě - v té druhé závorce opravdu nemá být sjednocení, ale průnik. Pak ti vyjde modrý interval a v průniku s "menší než -3" ti vyjde prázdná množina.
Z toho mého náčrtku paraboly je vidět, kdy nabývá kladných/nezáporných hodnot (-inf,-2] U [1,inf) a kdy záporných (-2,1) - to je ten můj modrý interval.
Pak tyto obory jen zkombinuješ s tou dřívější podmínkou:
pro x větší než -3 zůstane z intervalu (-inf,-2] U [1,inf) jen (-3,-2] U [1,inf)
a
pro x menší než -3 nezůstane z intervalu (-2,1) nic.
Výsledek je tedy snad už definitivně správně (-3,-2] U [1,inf).
Použil jsem hranaté závorky místo lomených, které zde na Poradně nefungují.
Moýná jste zaměnil iracionální a komplexní řísla. (A moýná bych byl taky opatrný s pojmem "řešení". Chápu to tak, že tazatel zkoumí funkci jedné proměnné a hledá její definiční obor. Žádné řešení rovnice, jaké asi zvaýujete vy, ho nezajímá.)
Nejenom možná, ale určitě. Chybička se vloudila. Zatím mám jiné důležitější starosti. Zdravíčko je zdravíčko
0x
x²+x−2 = (x−1)(x+2)
Klíčové body jsou −3, −2, 1
x = −3 je vyloučeno.
Na intervalu (−nekonečno;−3) je výraz pod odmocninou záporný (stačí dosadit třeba x= −10)-
Na intrvalu (−3, −2) je kladný (dosazením x = −2,5)-
Pro x = −2 je nulový.
Pro x z intervalu (−2, 1) je záporný (x = 0).
Pro x = 1 je nulový.
Pro x z inttervalu (1,+nekonečno) je výraz kladný.
Definiční obor Df = (−3, −2>U <1,+nekonečno)
Jasně, ja vim jak ma vychazet ten definiční obor (podle grafu). Jen mi nejde do hlavy, když to počitam moji metodou co jsme se učili, že mi to nevychazi. Jedine kdy mi to vychazi, tak že necham ten zapis hned co jsem daval na začátku, akorad změnim posledni podmínku x<-3 na x>-3. Ale moc mi to nedava smysl proč.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.