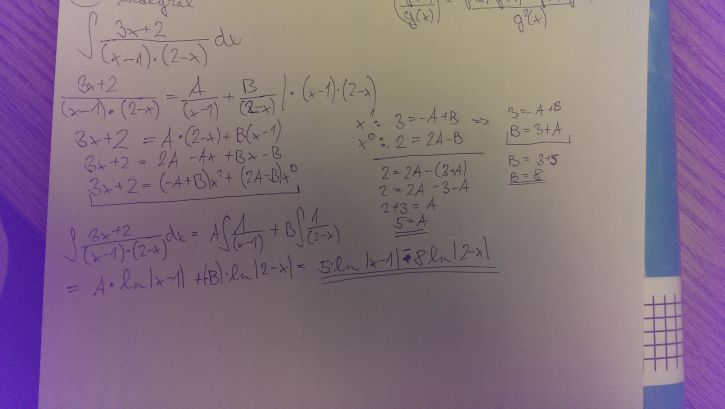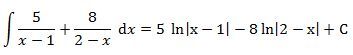Zdravim, potreboval bych poradit s timto integralem vyresil jsem ho avsak wolfram mi vyhodil jiny vysledek. Stejny az na parametr prvniho prirozeneho logaritmu. Vysledky jsou rozdilne (muj a od WA).
Postup a odka na Wolfram prikladadam zde, na konci jsem provedl u druheho ln substituci, proto to -
Integral (3x +2)/((x-1)*(2-x))
Dekuji moc vsem za rady Filip,
doplněno 07.01.17 19:40:
Omlouvam se za obrazek.
2x
B by mělo být -8
doplněno 07.01.17 20:12:
Jde o to, že v jednom jmenovateli je (2-x) a ne x-2. Zkus tedy celý zlomek rozšířit -1. V čitateli bude (-3x-2) a pak snad A vyjde s mínusem.
Jinak zkus zakrývací metodu, u takhle jednoduchých zlomků píšeš pak rovnou A=..., B=...
doplněno 07.01.17 20:30:
Nebo jak radí x. Mínus se vytkne až při integraci.
Diky za odpoved, to mi nejak nesedi 
. Muzete to hodit na papir? Pokud bych moc nezdrzoval? Dekuji.
Diky presne nad tim minusem u nezname jsem premyslel. Ale nikdo nam o tom nic nerekl. Takze vzdy upravit tak, abych mel soucin korenovych cinitelu s kladnou neznamou ano? Pokud by neznama v zavorkach byla zaporna, tak mi spravne ty parc. zlomky vyjit nemouzou ano?
doplněno 07.01.17 20:24:
Mohl by mi to nekdo stoprocentne potvrdit? Treba Kartaginec nebo nekdo jiny? Dekuji 
Máš ten výsledek správně, wolfram taky.
Wolfram definuje integrál/...
doplněno 08.01.17 13:18:
Tvůj výsledek platí ve všech intervalech, kde je integrál definovaný
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.