Dobrý den, v čem prosím dělám chybu při výpočtu vlastních čísel (nemůžu ji najít)? Děkuji
3x
Předposlední řádek: má být +9λ2
doplněno 01.01.17 14:49:
Také: -λ3
doplněno 01.01.17 14:57:
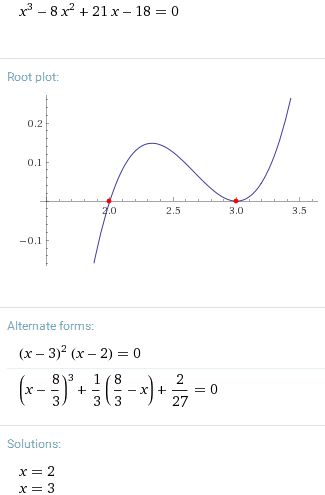
Wolfram radí, že to pak jde upravit.
Už jsem nad tím trošku přemýšlel dříve, ale dnes bohužel není mozková kůra schopna nic vymyslet.
Snad se zde zastaví někdo chytřejší nebo vyčkat do zítra.
Tady na papíře mi to vyšlo, ale je to vysloveně náhoda, protože ty kořeny jsou takové hezké. Pro obecné kořeny by můj postup nefungoval.
Můj postup: Všiml jsem si podobnosti tvaru rovnice se vzorcem pro (x-y)3 a kvůli koeficientům u x2,x a absolutního členu bylo jasné, že y nebude 1, ale spíše něco kolem 2-3. Zkusil jsem nejdříve rozvoj pro y=2, doplnil chybějící členy, aby to odpovídalo původní rovnici a po úpravách se podařilo vytknout (x-2) z celé levé strany. Zbytek už pak šel upravit na (x-3)2.
Ze zájmu jsem pak zkusil stejný postup pro y=3 a ten je mnohem jednodušší (protože 3 je dvojnásobný kořen, tak (x-3)3 vymete po celkovém vytknutí (x-3)2 z celé levé strany už všechny členy vyšší než x1).
x3 - 8x2 + 21x - 18 = 0
(x-y)3 = x3 - 3x2y + 3xy2 - y3
pro y=3:
x3 - 3x2.3 - 3x.32 - 33 + x2 -6x + 9 = 0
(x-3)3 + x2 -6x + 9 = 0
(x-3)3 + (x-3)2 = 0
(x-3)2.(x-3+1) = 0
(x-3)2(x-2) = 0
Jak je vidět, úprava funguje, jen když se člověk trefí přímo do kořenu.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.