Zdravím, mám takový problém s jedním prikladem.
Mám určit globální extrém u funkce dvou proměnných.
Mám to cellekm hotový, akorát jedna část mě nevychází.
A to část kdy dělám dolní půlkruznici.
Tedy tu rovnici kruznice dolní část jsem mám dosadit do zadání. To jsem udělal. Pak to mám zderivovat coz jsem uděla. A pak polozit rovno nule a po upravach mi to nevychazi.
Tak jestli by mi s tim někdo pomohl. Díky.
blbost mam to blbě pošlu znovu, ja poslal verzi horni pulkruznice, ja měl za y dosazovat i s minusem pred odmocninou. :D
pookud jsem za y dosadil tu odmocninu spravně a je to dobre zderivované, tak muzu tu rovnici pak vynasobit jmenovatelem, jak jsem to udelal?
Takto nelze postupovat! Na jedné straně ponecháte výraz s odmocninou a na druhé straně rovnice budete mít trojčlen. Pak můžete obě strany umocnit.
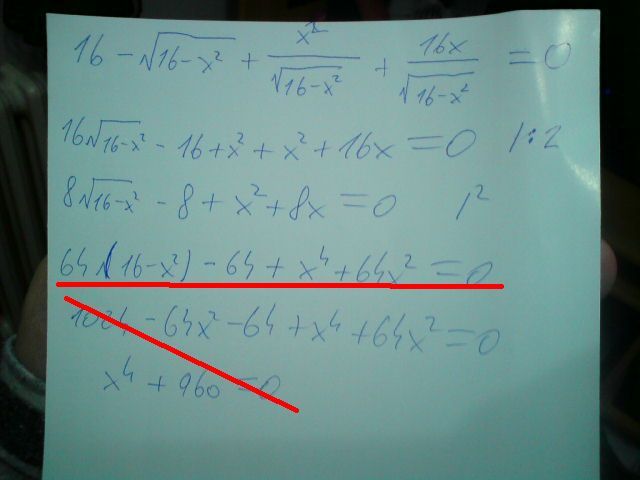
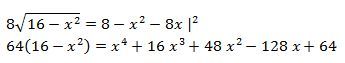
aha, takze kdyz jsem to samé dělal u horní pulkruznice a dělal to samé a vyšlo mi to samé (az na znaménka, ty jsem zvýraznil červeně). A kdyz jsem právě pokračoval stejným zpusobem, tak mi vyšlo x4 + 128x2-1088=0
x2 =t diskriminant ...a vyšlo mi právě ze x,y =odmocnina z 8. coz má vyjit dle vysledku. Takze nahoda asi co. Mel jsem to udelat i predtim tim co pišete vy ten trojčlen.
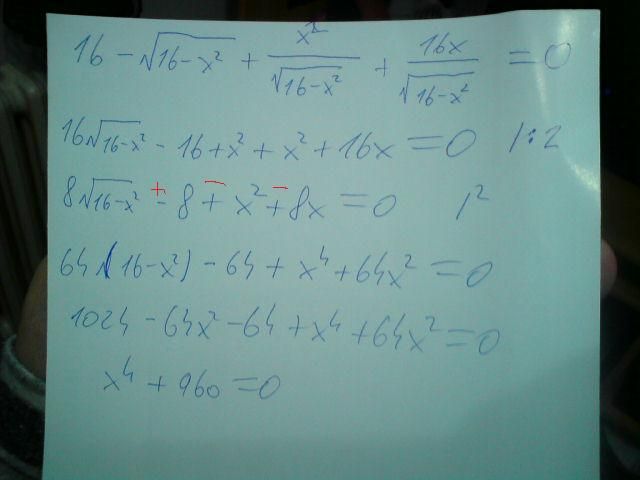
Zkoušel jsem tu rovnici s x4 spočítat v ruce a není to vůbec jednoduché. Nebýt toho, že se tam dá něco šťastně povytýkat a rozložit, tak by to asi nešlo vyřešit vůbec.
Pro představu: rovnice jde upravit na tvar
(x2 - 8).(x2 + 16x + 120) = 0
Druhá závorka se dá napsat jako (x + 8)2 + 56, tedy je to parabola posazená o 8 doleva, ale hlavně o 56 nahoru a proto neprotíná osu x a nemá reálné řešení. Lze pochopitelně zjistit i výpočtem přes diskriminant.
První závorka dává samozřejmě to řešení ±√8.
doplněno 17.11.16 02:01:
Pro jistotu upřesním: řešil jsem pochopitelně tu správnou rovnici
64(16 - x2) = x4 + 16x3 + 48x2 - 128x + 64
0x
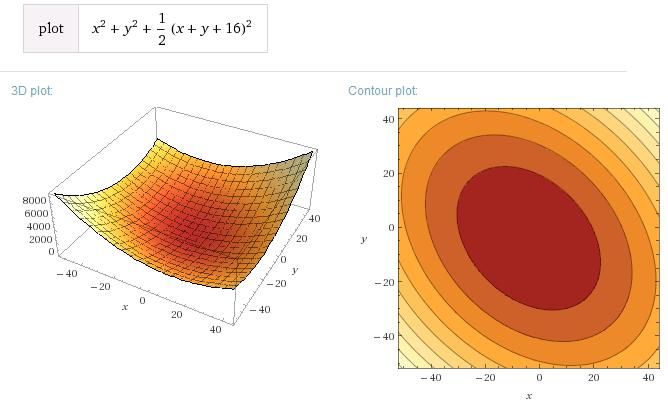
Pro představu, jak ta funkce vypadá ( vykreslil WolframAlpha):
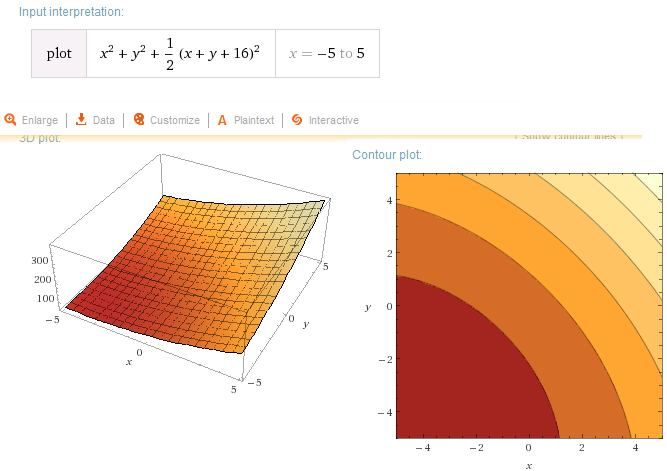
doplněno 17.11.16 03:55:
Přidán ještě jen rozsah -5 odkaz na originál od Wolfram).
Dále zeleně vyznačen průmět koule x2 + y2 <16 a modře řez pro řešení (±√8 ≈ ±2,8).
doplněno 17.11.16 04:01:
Mělo být:
Přidán ještě jen rozsah -5 ≤ x ≤ 5 ( odkaz na originál od Wolfram).
Dále zeleně vyznačen průmět koule x2 + y2 ≤ 16 a modře řez pro řešení (±√8 ≈ ±2,8).
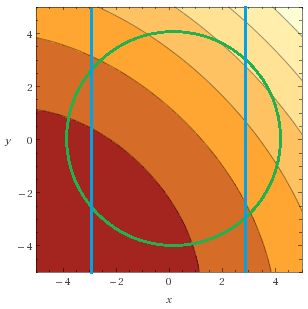
vyznačen průmět koule
Omlouvám se - ne průmět koule, ale obrys kruhu 
Mimochodem, jestli to má být kružnice, tak ta má rovnici x2 + y2 = 16 a ne x2 + y2 ≤ 16 (to je kruh = "kružnice s vnitřkem").
My bereme jen tu spodní polovinu kružnice.
Je vidět, že to řešení v bodě +√8 nebude globální minimum (naopak ta hodnota v -√8 bude).
0x
Ten postup dosazováním do funkce a děláním z ní funkci jedné proměnné mi přijde dost neelegantní. Lépe je použít standardní postup na hledání extrémů funkcí více proměnných. Nejdřív najít lokální extrémy ( lide.uhk.cz/...), ten je jen jeden [-4,-4] a leží vně kruhu. Potom pomocí metody Lagrangeových multiplikátorů ( lide.uhk.cz/...) lze najít vázané extrémy na kružnici. Z Lagrangeových multiplikátorů lehce vypadne, že x=y, a dosazením do rovnice vazby lehce získáme 2x2 = 16, a tedy i body [-2*sqrt(2),-2*sqrt(2)] (minimum) a [2*sqrt(2),2*sqrt(2)] (maximum).
To je sice hezké, ale ne každý absolvoval 2 semestry Analýzy funkcí více proměnných, ještě méně lidí to pořádně pochopí a umí použít a ještě méně lidí to odpřednáší. 
Tento postup jim asi poradili ve škole a časem se propracují třeba i k těm multiplikátorům. Nebo taky ne a rádi to ponechají lidem, pro které je matematika životem.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.