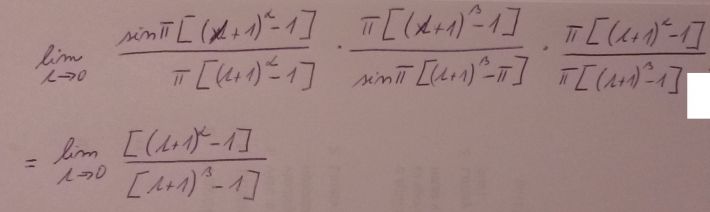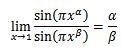Dobrý den, jak se prosím vypočítá tato limita? Využila jsem významné limity x-->1 sinx/x = 1
Nevím, jak dál. Děkuji
3x
V lastně i to je rozumné. Nejjednodušší je L(Hospitalovo pravidlo, máte ho k disposici? Jestli ne, zkusíme to jinak-
Nemáme ho používat, že by to bylo moc jednoduché a pak že bychom se setkali s příklady, kde nejde použít.
Mockrát děkuji
S tímhle přístupem mohu jen souhlasit.
Ty úpravy, které jste uvedla teď, jsou dobré. I zde je na závěr teoreticky možné použít L´Hospitalovo pravidlo. Pokud
se mu chceme vyhnout, lze použít Taylorův rozvoj, což v našem případě je více méně diferenciál. Anebo lze zlomek ze závěrečné limity rozšířit t, následně pak počítat limity výrazů [(t+1)α−1]/t, resp. totéž pro beta, a to je vlastně derivace xα v bodě x = 1, resp. podobně pro beta.
Je to prosté:zderivujete xα (jako α x α −1) a dosaadíte x = 1.
Když se zamyslíme, tak derivaci funkce f = f(x) primárně definujeme jako derivaci v nějakém pevném bodě, třeba v bodě x0, jako limitu podílu [f(x)−f(x0)]/[x − x0] pro x blížící se k x0 (tedy jako číslo), respektive alternativně jako limitu podílu [f(x0+t) − f(x0)]/ t pro t blížící se k nule (což odpovídá té vaší poslední limitě, pokud čitatele i jmenovatele vydělíte t) a teprve následně zavádíme derivaci jako funkci jednoduše tak, že definici derivace v bodě aplikujeme na všechny body, pro které to je možné.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.