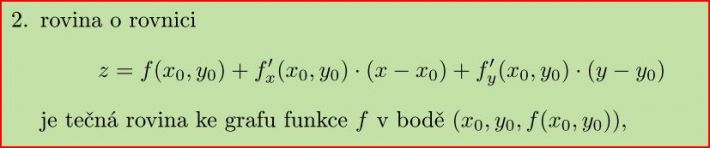Nejste přihlášen/a.
Zdravím, je tu někdo kdo by mi byl schopný vysvětlit diferenciál u funkcí dvou proměnných? Kdy je funkce diferencovatelná...
2x
Noo právě na funkci jedné proměnné jsem to pochopil, akorát si to neumím predstavit moc geometricky no :D
Ted mi to vypadlo, kdx mají nebo jak poznám ze funkce má parciální derivace spojité?
No jak zjistit spojitost derivací? Standardně tak, že je spoštu a pok vyšetřuji jejich spojitost jako u kačdé jiné funkce,
A k té geomefrické představů: obecně graf lineární funkce dvou proměnných je rovina, procházející počátkem No a kdyř si v prostoru vezmete funkci F(x,y). položíte počátek souřadnic do bodu (x0,y0,F(x0.y0)) a nové proměnné budee značit dx, dy, tak graf bude tešná rovia je grafu F. A chcete.li tečnou rovinu vyjádřit jako funkci promenných x, y, tak místo dx a dy budšete psát x–x0. místo dy přírůstek y a tečná rovina bude z = F(x0,y0) + dF
Ještě bych navázal na takovou maličkost, jak dostanu tu parametrickou rovnici té normály.
Ze sš si pamatuju z čeho se skládá, jde mi o ten směrový vektor zde uvedený. Jak je psáno tak je to současně normálový vektor té roviny.
Rovnici roviny zde taky mám napsanou, ale jak z ní ten normálový vektor vyčtu? Díky
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.