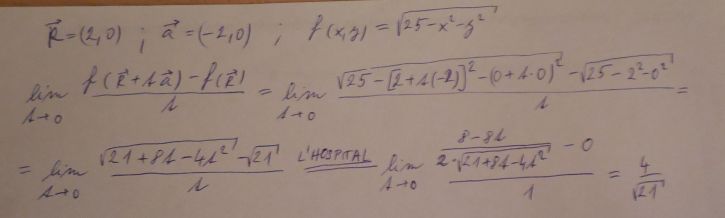Zdravím, chtěl bych poradit, kdyz mám vypočítat derivaci v nějakém bodě A ve směru vekoru u.
Existuje zpusob pomoci gradientu, to ale ještě nevím ani nechci.
Jde mi o způsob pomocí predpisu limity. vlastne mám A+tu parametrická rovnice prímky, tu rozlozim na x0 +tu1
a y0 + tu2 a pak do te funkce dosadim za x a y a budu derivovat funkci o jedne nezname t.
Ale co dál? Mám tu derivaci t pocitat v nule? a proc?
Napr ten príklad b) pro prvni bod mi vyslo 4/ sqrt(21)
2x
Ano, těch 4/sqrt(21) by mělo být správně. Derivace se počítá v nule, protože tak je derivace definovaná. Derivace ve směru v daném bodu je rozdíl funkční hodnoty v bodu, který vznikl malým úkrokem z daného bodu o ta, a funkční hodnoty v daném bodu, to celé děleno t. To, že je ten úkrok infinitezimální, vyjadřuje limita pro t jdoucí k nule. Je to podobné jako při normální derivaci funkce jedné proměnné, ta se také počítá pro t jdoucí k nule.
Ten příklad b) pro bod R je na obrázku níže. Do funkce f prostě dosadím za x první souřadnici vektoru R+ta a za y tu druhou. Při výpočtu jsem použil LHospitalovo pravidlo. I když pomocí toho gradientu je to jednodušší 
.
Bylo by to správné, až na maličkost.
Dříve, než zahájíme výpočet zadané derivace, musíme vždy ověřit, že vektor definující směr má jednotkovou délku. V uvedeném příkladu vektor definující směr není jednotkový – | a | = 2
http://artemis.osu.cz/mmpom/MathCad%5Cmc_2_3.html
Já vycházel z tohoto math.feld.cvut.cz/..., viz Poznámka 5.2. i), tam má jinou definici. Záleží na tom, jak mají směrovou definici zadefinovanou. I když uznávám, že je logičtější nejdřív ten vektor znormalizovat.
Nebude-li mít vektor definující směr jednotkovou délku a neznormalizujeme ho, pak ale neplatí, že derivace je rovna tg(α ).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.