Ahoj,
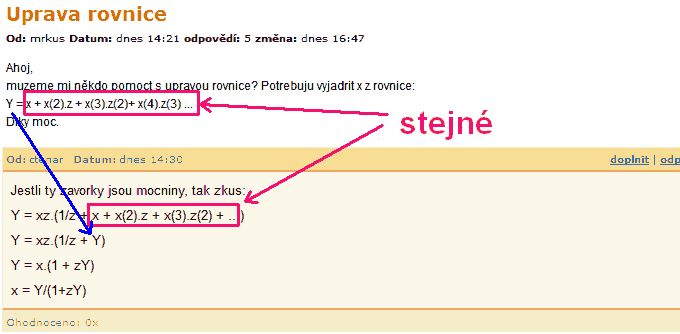
muzeme mi někdo pomoct s upravou rovnice? Potrebuju vyjadrit x z rovnice:
Y = x + x(2).z + x(3).z(2)+ x(4).z(3) ...
Diky moc.
0x
Jestli ty zavorky jsou mocniny, tak zkus:
Y = xz.(1/z + x + x(2).z + x(3).z(2) + ...)
Y = xz.(1/z + Y)
Y = x.(1 + zY)
x = Y/(1+zY)
Očekával bych, že Y a z jsou známé (znáš jejich hodnotu), proto chceš vyjádřit ("dopočítat") x. Jinak by to asi nemělo smysl nebo tomu nerozumím.
Počkej si, co sem přijde poradit @kartaginec nebo @x .
Y neni x x(2).z x(3).z(2) ...
Já vím, že není. Netvrdil jsem to. Nevím, kde jsi to vzal.
Y je x + x(2).z + x(3).z(2) ... Sám jsi to napsal v zadání. Já to jen dosadil do té závorky. Nebo mi něco uniká?![]()
Ted me napada, neda se to zapsat jako nejaka posloupnost? Aby ta rada tam nemusela byt nekonecna?
x + x(2).z + x(3).z(2)+ x(4).z(3) = Σxk+1zk pro k=0..∞
doplněno 04.10.16 19:27:
Jen bych chtěl zkusit jiné formátování: ∑k=0∞xk+1zk
0x
Ano, je to mocnina. Uz je mi to jasne, jsem idiot..zda se. Jeste se ujistim, ze jsem ten priklad vubec dobre upravil. Snazil jsem se co nejvic konstant nacpat prave do toho Y, aby to bylo prehlednejsi. Jinak ctenarovi moc dekuju a smekam pomyslny kloboucek!
Čtenáře by @kartaginec strčil do kapsy kdykoliv, kdyby se mu zachtělo. ![]() Tuto otázku jsem jen prostě viděl dříve než on. Toť vše.
Tuto otázku jsem jen prostě viděl dříve než on. Toť vše.
Treba a mozna by to kartaginec podobne nevyresil. Z odpovedi tusim, ze mu matematika rika pane. Takový clovek ale naopak casto prehlidne to nejjednodussi reseni, pac uvazuje ve vyssich sferach zivota a smrti. Pak nastupuje "selsky rozum" a prirozeny duvtip ctenare. Treti do party je blbecek, co sotva prolez zakladkou, a musi oblizat metamaticka fora. Bez takovych by ale nebylo kartagincu, uz vubec ne ctenaru.
Vazeny ctenari
co tahle rovnice (malinka uprava - opet vyresit neznamou x):
Y=x + (1-x)(2) .z + (1-x)(2) .z(2) .x + (1-x)(2) .z(3) .x(2)...
pricemz (2) je zase mocnina
To je to samé v bleděmodrém ![]() :
:
Y=x + (1-x)2z + (1-x)2z2x + (1-x)2z3x2 + ... = x + (1-x)2(z + z2x + z3x2 + ...) = x + (1-x)2zx.(1/x + z + z2x + z3x2 + ...)
a z toho už zase se opakuje
z + z2x + z3x2 + ...
a z rovnice
Y = x + (1-x)2(z + z2x + z3x2 + ...)
snadno odvodíme, že
z + z2x + z3x2 + ... = (Y-x)/(1-x2)
Po dosazení do
Y = x + (1-x)2zx.(1/x + z + z2x + z3x2 + ...)
vyjde
Y = x + (1-x)2zx.(1/x + (Y-x)/(1-x2))
Y = x + z.(1-x2 + xY - x2)
(-2z)x2 + (zY + 1).x + (z - Y) = 0
a to je kvadr. rovnice tvaru
ax2 + bx + c = 0
Snad jsem tam někde neudělal chybu. Překontroluj si to.
0x
Druhá možmost je na rovnici Y = x(1 + zx + (zx)² + (zx)³ + ... ) otrocky pouřít vzorec pro součet geometrické řady s kvocientem q = xz, platný pro |zx | <1:
Y = x / (1 −xz) , respektive zY = W = zx/(1−zx).
Vyřešením této rovnice dojdeme ke vzorci, který už známe, ale který je validní pouze pro Y, která odpovídají té podmínce na kovcient. A poněvadž vidíme, že výše vypsaný vzorec definuje hyperbolu s osami W = −1, u =zx = 1, z níž ovšem musíme brát jen omezený definiční obor a odpovídající obor hodnot, snadno zjistíme, že originální úloha je řešitelné pro zY větší než −½.
(Pro jednodušší zápis jsem oznašil (zavedl substituci) zY = W, zx = u a vyčetřoval jsem průběh finkce W = W(u).)
Vidíš, co jsem říkal?
Na druhou stranu tě může potěšit, že s velkou pravděpodobností budeš vydělávat více než lidi jako on. Tak to bohužel chodí.
Vysvětlení té hyperboly:
vyšetřuje zY = xz/(1-xz)
neboli W = u/(1-u)
úpravy: W = -u/(u-1) = (-u + 1 - 1)/(u-1) = [-(u - 1) - 1]/(u - 1) = [-(u - 1)/(u - 1)] - 1/(u - 1) = -1 -1/(u-1) = -[1/(u-1)] - 1
tedy funkce tvaru y = 1/x, jejímž grafem je hyperbola, která je akorát:
- výškově převrácená kvůli tomu mínus před zlomkem
- posunutá o 1 doprava, kvůli té 1 v (u-1)
- posunutá o 1 dolů, kvůli té -1 na konci výrazu
Protože xz (neboli u) musí být podle defin. oboru>-1,
W (tedy zY) nabývá hodnotu:
W = u/(1-u) = -1/(1-(-1)) = -(1/2)
Přesně jak píše @Kartaginec ![]()
doplněno 05.10.16 15:28:
Na druhou stranu - kartaginec asi vyšetřoval asymptoty hyperboly přímo z její středové rovnice a ne kreslením grafu jako jsem to ukazoval já výše.
Mě po úpravě W=u/(1-u) vyšlo:
(u-1).(W+1) = 1
protože (u-m).(y-n) = c
pak
m=1; n= -1
asymptoty: u = m = 1; W = n = -1
Velice pěkné řešení.
Jen doplním, že jako geom. řadu lze počítat přímo ze tvaru v zadání, kdy a1 = x; q = xz. Vyjde to pochopitelně stejně.
Graf mi vyšel stejně (pěkný trik s tím rozšířením pomocí z !) a i WolframAlpha souhlasí. Pravá větev hyperboly se vůbec nepoužije vzhledem k definiční podmínce |xz| = u <1
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.