Zdravím,
mohl by mi prosím někdo poradit se třemi příklady? Potřebuji určit, zda je posloupnost rostoucí nebo klesající a dokázat to.
Příklady jsou v příloze.
Vím, že 1) má být klesající, 2) taky klesající a 3) rostoucí, ale nevím, jak to dokázat. Dělají mi problém ty mocniny/odmocniny a nejsem si jistý výsledkem.
Díky za každou pomoc.
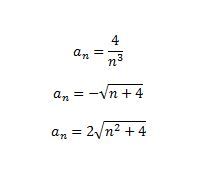
0x
Posloupnost je klesající pokud an-an+1>0
(4/n³)-(4/(n+1)³)
Spočítej. Pokud je výsledek větší než nula pak je posloupnost klesající.
Obdobně pro rostoucí
doplněno 17.09.16 14:10:
Tady nejde o výpočet. Podstata je posoudit zda výraz je vetší než nula pro každé n
doplněno 17.09.16 14:24:
Třeba v tom prvním případě bude jmenovatel druhého dvojčlenu vždycky větší než n³ takže druhý zlomek bude vždycky menší než první zlomek a výsledek bude tedy vždycky kladný
Díky. Postup znám, jen prostě nevím, co přesně dělat s těmi odmocninami, vycházejí mi úplné šílenosti.
Třeba u toho prvního (byť tam odmocniny nejsou) mi vychází kvadratická nerovnice 3n3 + 3n + 1> 0.. Diskriminant je tedy záporný (-3). Tím pádem ale tato nerovnice nemá řešení, protože záporný diskriminant toto znamená, ne?
Co to?
Jednak 3n3+... není kvadratické, ale kubické, a pokoušet se tam tedy o nějaké diskriminanty, ...
A jednak mi vyšlo n3+3n2+3n+1>0 (snad jsem se nepřepočítal).
Každopádně oba výrazy (tvůj 3n3+3n+1 i můj n3+3n2+3n+1) jsou určitě větší, než 0, předpokládáme-li "n" kladné celé (což můžeme, když je to přirozené číslo).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.