Zdravím, nechápu poslednímu řádku té nerovnosti -kde se vzala a to znázornění na obrázku díky za vysvětlení.
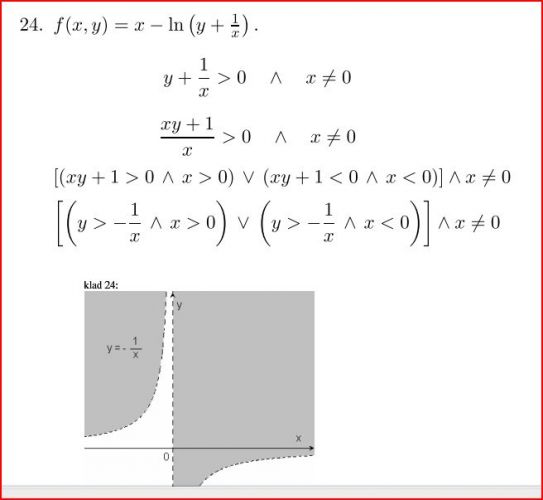
To je jen částečná odpověď a týká se té poslední podmíny. To před tím v hranaté závorce odpovídá tomu, že argument logaritmu musí být kladná, a ty obrézky ukazují oblast v níř je tato podmínka splněna čárkované linie představují body, pro něž je argument roven nule).
0x
Po pravdě to řešení zde uvedené v rámečku se mi vůbec nelíbé. Není chybné, ale řečitel prování nesmyslné nadbydečné operace, které následně zase pracně neutralizuje, a co se táče závěrečné formulace definičního oboru, nesprávně to není, ale není to hotové, Kdyby mi takovýhle výpořet donesl můj student, tak bych mu to vrátil k dalčám zjednodučujícím úpravám. Kde jste proboha k tomu přišel?
Přikládám obrázek, jak by mohlo řešení vypadat.
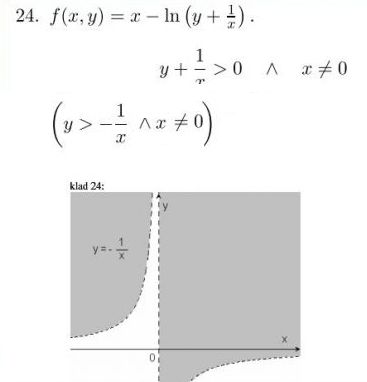
jsou to řešené příklady ze skript z VŠ a právě kdyz na začátku je zápis stejný akorát v první podmínce je menší a v té druhé je větší. No a o řádek níž jsou ty nerovnice stejnéé.
Protože v té podmínce je x<0 a když vyjadřujeme y, tak dělíme záporným číslem (x<0 ) a při dělení záporným číslem se obrací znaménko nerovnosti.

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.