Zdravím, potřeboval bych pomoct s nějakým příkladem.
Nedávno jsem procvičoval obsah, objem tělesa rotujícího podle osy x.
Teď jsem chtěl počítat typy, kdy ten útvar rotuje kolem osy y, ale vůbec nevím jak na to, vypočítal jsem jenom 3 příklady ze všech.
jedná se o příklady, které mi zaslal Kartaginec 
a jsou to ty úplně poslední - šesté zadání. Mám jen a), p) r)
Tak jestli by mi to někdo vysvětlil třeba na tom příkladě b).
2x
A o co konkrétně vám jde? Víte, jak vypadá integrál, který máte počítat, a jen ho neumíte spočíst, nebo je problém v určení integrandu?
No, koukám, že #x mezitím napsal dost podrobnou odpověď, tAKŽE MÁ POZNÁMKA UŽ JE MOŽNÁ OFF TOPIC.
Spíš asi co mám integrovat
doplněno 22.07.16 18:26:
Nebo tak, nevím kde se v tom prvním případě vzalo 2pí a v tom druhém případě ten začátek toho vzorce před integrálem
A tu inverzní funkci k funkci y=x2-x-6 určím jak?
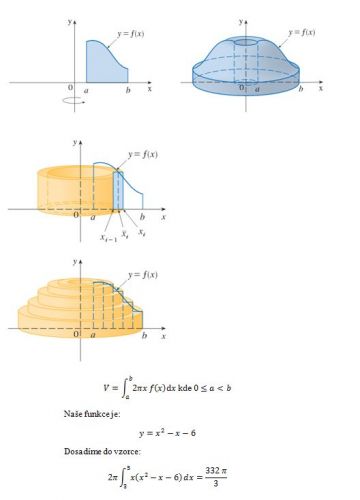
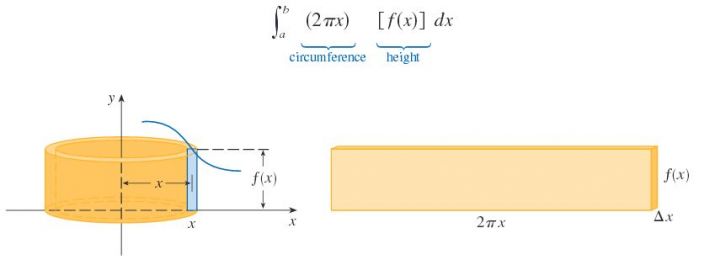
2π se tam objevuje, jelikož počítáme délku kružnice o poloměru r.
o = 2πr ... po vynásobení výškou válce dostaneme povrch pláště válce. Budeme předpokládat, že plášť válce je tenká slupka o tloušťce dr. Pak objem slupky je
V = 2πrh dr
Celé těleso se dá rozložit do mnoha velmi tenkých slupek. Sečtením jejich objemů dostaneme objem celého tělesa.
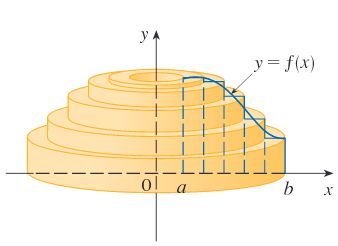
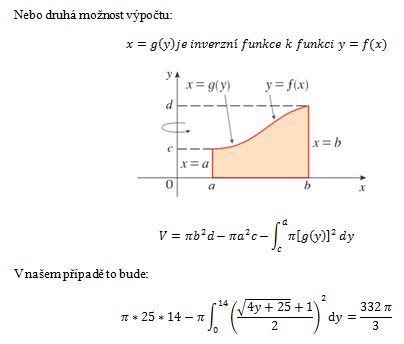
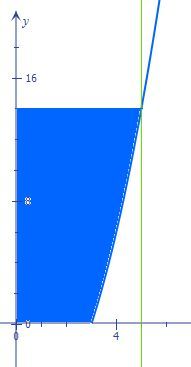
V tom druhém případě od objemu válce o poloměru r = 5 a výšce 14 (V = πr2h = π⋅52⋅14) odečteme objem tělesa, které vznikne rotací části paraboly (modrá část na obrázku), a tím získáme požadovaný objem.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.