Ahojda, potřebovala bych poradit, jak nakreslit tuto záležitost. Vubec nevim, jak mají ty šipky směřovat. Pokud budete někdo vedet, byla bych ráda za pomoc. Na mail ( M.Nosalkova@seznam.cz) mi muzete poslat nákresy, pokud vas neco napadne. Děkuji ![]()
0x
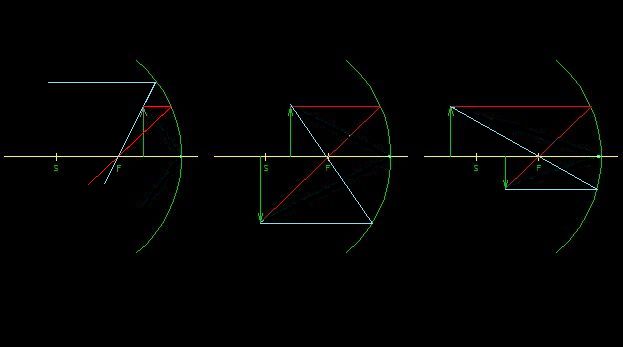
tady ty náčrtky máš. Jestli jsem dobře vyluštil tvůj obrázek, tak
A/ obraz šipky se nevytvoří
B/ obraz šipky bude zvětšený
C/ obraz šipky bude zmenšený
doplněno 08.05.16 09:25:
To co vidíte na obrázku, je nejzákladnější ze základních úloh konstrukce obrazu v dutém zrdcadle. Přesně ta, kterou tazatelka poptává. Červený paprsek jde z vrcholu šipky, je rovnoběžný s osou a odráží se do ohniska. Ohnisko F je v polovině mezi středem S a vrcholem zrdcadla. Modrý paprsek jde z vrcholu šipky rovnou do osy a odráží se ve stejném úhlu. Tam kde se protnou, najdete odražený obraz šipky.
Douška pro některé odborné poradce : Nastudujte si aspoň základy.
Douška pro některé odborné poradce : Nastudujte si aspoň základy.
My si je pamatujeme ze školy:
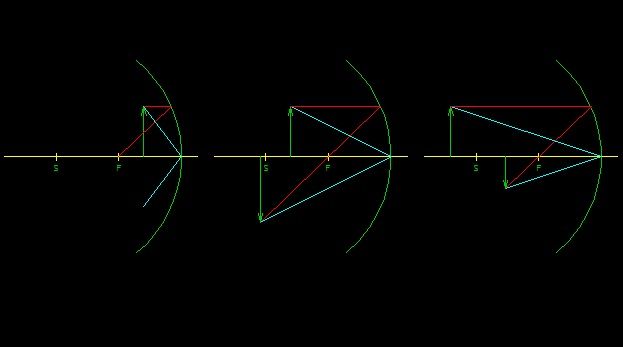
Při optickém zobrazování používáme tři význačné paprsky:
1. Paprsek procházející středem křivosti zrcadla má po odrazu od zrcadla opačný směr než měl před odrazem; tj. tento paprsek se odráží zpět do bodu C.
2. Paprsek rovnoběžný s optickou osou se od zrcadla odráží tak, že optickou osu protíná v bodě F.
3. Paprsek procházející bodem F se po odrazu od zrcadla šíří rovnoběžně s optickou osou.
Jak vidíš, vyšetřování odrazu paprsků ve "vrcholu"zrcadla se pro body mimo optickou osu neučí.
no dobře. Já mám nějaké znalosti optiky ze střední i zkoušku z optiky na vysoké a moc dobře si pamatuji, jak mizerně a nesrozumitelně ji vy kantoři vysvětlujete. Tazatelka poptává základní obrázek toho, jak duté zrdcadlo vytváří obraz.
Jestli chceš diskutovat, tak namaluj, naskenuj a hoď sem tvoje řešení. Ať ho vidím. A hlavně by ses mohl zaregistrovat.
doplněno 08.05.16 12:44:Jsem si to myslel. Tvoje první možnost zleva je ale lehce mimo mísu ne? A pro druhou a třetí možnost platí, že takových paprsků můžeš přidat dalších padesát a pokaždé ti vyjde totéž.
No a jen pro informaci. Můj náčrtek nahoře jsem nevymyslel já, ale jistý Isaac Newton. Znáš to jméno? Zdůvodnil tím nejjednodušším a nejpřehlednějším způsobem, jak duté zrdcadlo obraz tvoří a proč jej převrací.
Tak a dost. Howgh.
Chtěl jsem sem poslat dokreslené řešení toho zdánlivého obrazu v prvním případě už dlouho, ale bohužel jsem se k tomu nedokázal dostat. Proto tedy až nyní se značným zpožděním.![]()
Pro zájemce: všechny možné případy i s uvedením jejich řešení jsou uvedeny na této stránce.
doplněno 17.05.16 23:49:
Sakra, grafický program mi tam automaticky vložil prázdné místo, když jsem pracoval v blízkém náhledu.![]()
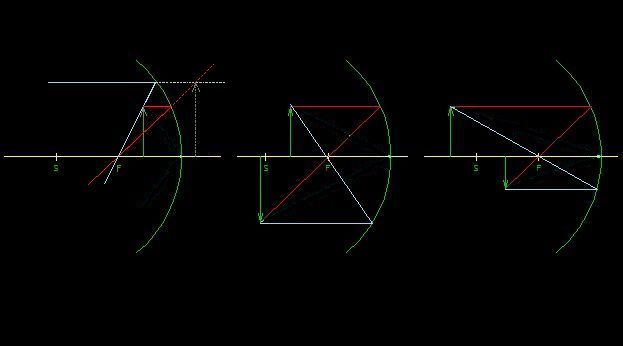
Což to by byla další možnost, asi jednodušší (není třeba měřit či jinak konstruvat ůhly, stačí spojovat body a kreslit rovnoběžky). Samozřejmě přweně to vyjde u parabolického zrcadla, u kulového zrcadla se t jen ÿu tři paprsky protnou v jednom bodě, jen pokud leří v Gaussově nitkovém prostoru. Ale možná bych upřesnil, že i v prvním případu se obraz objeví (jestli utvoří, toť otázka), ale bude zdánlivý.
0x
Ještě se k tomu vrátím, a začnu poznámkou, že striktně vzato, bez dalšího upřesnění, to má "špatně" jak figurek, tak čtenář; na druhou stranu v mezích přibližného řešení jsou oba jejich postupy v pořádku a rovnocenné, v souladu s tím, co se o tom běžně učí (ale učí se to s vědomím těchto omezení; třeba v Encyklopedii fyziky, kterou odkazuje čtenář,hned v úvodu čteme:V dalších úvahách se omezíme pouze na paprsky, které se nacházejí v blízkosti optické osy, v tzv.paraxiálním prostoru:PARAXIÁLNÍ PROSTOR JE TAKOVÝ PROSTOR SYMETRICKY ROZLOŽENÝ KOLEM OPTICKÉ OSY ZRCADLA (RESP. ČOČKY), V NĚMŽ JE ZOBRAZENÍ KOLINEÁRNÍ. TO ZNAMENÁ, ŽE PŘI ZOBRAZOVÁNÍ NEVZNIKAJÍ ŽÁDNÉ VADY.Kolineární zobrazení je zobrazení, při kterém se zobrazí bod na bod a úsečka na úsečku a ne na oblouk nebo jinou křivku.Jak široký paraxiální prostor budeme uvažovat, závisí na míře přesnosti, s níž chceme zobrazení definovat.. Ono totiž, jak praví Feynman ve svých Přednáškách, "geometrická optika je nejužitečnější aproximace pro praktickou konstrukci mnoha optických systémů apřístrojů. Geometrická optika je buď velmi jednoduchá nebo velmi komplikovaná. Tím myslíme, že ji můžeme studovat velmi povrchně a tak, abychom byli schopni zhruba narhnout přístroje s použitím pravidel, která jsou tak jednoduchá, že se jimi zde vůbec nemusíme zabývat (prakticky odpovídají středoškolské úrovni), , nebo chceme-li poznat drobné chyby čoček a podobné detaily, stává se tak složitou, že diskutovat o tm zde je příliš předčasné"Abych to trochu rozvedl: Feynmanova poznámka má váhu zejména u čoček, kde musíme počítat i se Snelliovým zákonem (a přesné návrhy třeba objektivů se dělají na počítačích), ale projevuje se i u zrcadel. kde jedinou potřebnou "středoškolskou znalostí" je zákon odrazu. Pro kulové zrcadlo a konstrukci odražených paprsků (a následně obrazu v zrcadle) to znamená toto: označíme-li si S střed zrcadla, pak paprsek p, který dopadne na zrcadlo v bodě T a svírá s poloměrem ST úhel α, se odrazí tak, že odražený paprsek svírá s tímto poloměrem stejný úhel, ale symetricky. Speciálně paprsek, jdoucí středem S, se odrazí zpět po vlastní dráze, paprsk, dopadající do vrcholu zrcadla, se odrazí symetricky podle optické osy (ale optickou osu si mohu vlastně zaměnít s libovolným poloměrem) – to jsou dvě nesporná fakta – a paprsek, jdoucí rovnoběžne s optickou osou pod úhlem α k poloměru, se odráží (pod stejným úhlem) a protíná optickou osu v jakémsi bodě F (α ) ve vzdálenosti f(α ) od středu. I to je pravda, ale zde je jeden zádrhel: středoškolská geometrická optika tvrdí, že f(α ) = r/2, kde r je poloměr zrcadla, a říká mu ohnisko. Následně pak tvrdí, že paprsek, jdoucí tímto ohniskem, je vlastně opačný k tomu rovnoběžnému a odráží se rovnoběžně s osou. Nuže, prozradím sladké tajemství: tohle není pravda. Jednoduchá úvaha říká, že f(α )= r/(2 cos α ), což je vždy větší než r/2 krom případu paprsku, splývajícího s optickou osou, a tvrzení o paprsku, jdoucím ohniskem, tak poněkud ztrácí smysl. Celá ta "velmií jjednoduchá aproximativní geometrická optika" je založena na tom, že klade cos α = 1, což lze udělat přibližně s přesností závislou na tom, jak úzký je výše zmíněný paraxiální prostor, tedy s jak malými úhly α pracujeme. Ostatně každý uživatel TV ví, že rovnoběžný svazek paprsků dokáže do ohniska soustředit právě a jen parabolické zrcadlo. No a teď k těm používaným "význačným paprskům": právě výše citovaná encyklopetie o nich říká" Tyto paprsky nejsou význačné tím, že by pro ně neplatily fyzikální zákony. Paprsky se chovají podlezákona odrazu. Mají ale takový směr, že lze snadno určit jejich směr po odrazu od zrcadla.a mluví o třech: paprsek jdoucí středem, paprsek rovnoběžný s osou a paprsek jdoucí ohniskem. Paprsek, odražený ve vrcholu zrcadla, skutečně pěkně ukazuje důvod, proč je skutečný obraz převrácený (a zdánlivý je přímý), ale u autorů encyklopedie prostě nepročel z hlediska konstrukční jednoduchosti.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.