Ja som to dala takto.ake vôbec neviem,či to mám správne ..
OR=v-u
NR=...neviem
KS=w-v
1x
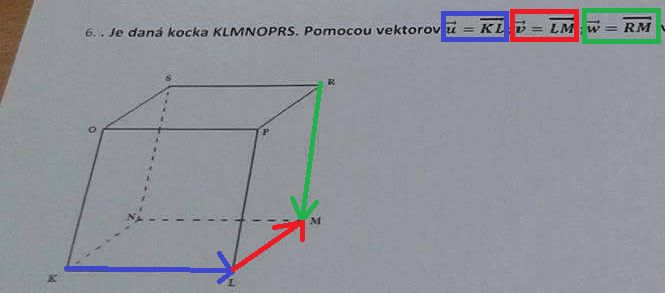
Nakresli si ty vektory u,v,w včetně šipek každý jinou barvou do té krychle.
Vektor ma velikost ("délku") a směr ("kam ukazuje")
OR = u+v
u+v je vektor KM a jeho velikost a směr je stejný jako vektor OR
NR = u-w
-w proto, že musíme vzít vektor mířící opačně ("na druhou stranu"); vyjde vektor KP, který má stejnou velikost jako NR
KS = v-w
obdobné vysvětlení
Snad to mám dobře. Nelíbí se mi tam to jiné umístění mojich výsledných vektorů v prostoru (absolutní pozice počátku vektoru). Kdyby to třeba byly vektory sil působící na těleso, tak by nebyly stejné 
Je rozdíl tahat za horní a spodní roh marshmallowové krychle 
doplněno 28.04.16 13:59:
Jen ještě upřesním svůj popis:
... vyjde vektor KP, který má stejnou velikost a směr jako vektor NR.
Vektor LR, který má stejnou velikost a směr jako vektor KS.
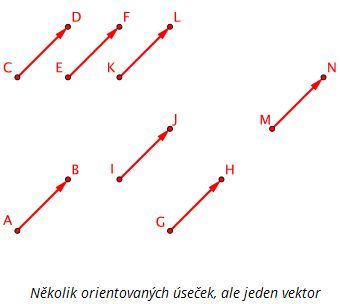
Je třeba si uvědomit, že nenulový vektor je množina všech orientovaných úseček, které mají stejnou nenulovou velikost a stejný směr.
Z toho jsem vycházel, že vektor je dán jen velikostí a směrem a že (x,y,z) umístění se v definici neobjevuje.
Jen mi nebylo jasné, jak do toho zapadalo různé momentové působení sil třeba na páce, ale teď mi dochází, že jsem motal 2 různé věci dohromady.
Máte to samozřejmě dobře.S tím rozličným počátkem si nedělejte hlavu. Základní definice vektoru, tak jak jste ji napsal a používáte (Vektor ma velikost ("délku") a směr ("kam ukazuje")), se týká tzv. volného vektoru. Takový volný vektor si lze představit jako jakýsi "mrak šipek", každá z nich ho plně charakterizuje a lze ji chápat jako, řekněme, konkrétní realizaci, chcete-li. umístění, a dvě různé šipky určují tentýž vektor, jestliže jsou rovnoběžné, stejně dlouhé a stejně orientované (akademik Eduard Čech ve své Analytické geometrii to popisuje jednoduše: dva vázané vektory AB ("šipka od bodu A do bodu B") a CD reprezentují tentýž volný vektor, jestliže střed úsečky AD je tentýž, jako střed ůsečky BC- A . V tomto smyslu například v našem zadání vektory KL. NM, OP i DR reprezentují tentýž (volný) vektor u a v tomto smyslu je zadání míněno.Samozřejmě, pokud pracujeme z vektory síly a zkoumáme jejich účinky na těleso, pak tyto účinky budou jiné, jestliže vektory působí v těžišti tělesa (pak se snaží posunout jěleso jako celek), nebo někde na okraji, kdy se snaží těleso navíc roztočit. S tím si fyzika poradí tak, že pracuje s pojmem vázaného vektoru, které máá krom velikosti a směru zadáno ještě působiště, ale to je z jiné opery. Tak to napsal i @x, jen jinými slovy. A netrapte se tím, že byste motal různě věci dohromady, spíš jde o různé stránky, vycházející z téhož základu, ale akcentující různé vlastnosti.
Volný a vázaný vektor ... slyším to poprvé a ujišťuji se, že pořád je se co učit.
Jak jsem psal, teoreticky mi to bylo jasné (velikost, směr), prakticky se mi ale při představě velkého množství vektorů v prostoru vybavují hned vektorové funkce více proměnných a jejich toky plochami nebo divergence na křivkách v prostoru. 
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.