Nejste přihlášen/a.
Dobrý den, chtěla bych požádat o pomoc s rovnicí : 3x(5)-7x(4)+5x(3)+5x(2)-7x+3; kde čísla v závorkách jsou exponenty a rovnice se řeší v oboru C. Dostala jsem se k substituci a dál nevím jak. Děkuji za pomoc.
1x
Přiznám se, že tohle jsme ještě nebrali, ale ze zvědavosti jsem to zadala do vyhledavače a podle rovnice.kosanet.cz/... je kořen všech rovnic o lichém počtu členů -1. Ale jak říkám, nebrali jsme to a tohle je jen takový výstřel do prázdna. ![]()
P.S. V zadání rovnice chybí pravá strana...
doplněno 09.02.10 18:01:KAždopádně, asi toho z těch stránek pochopíte víc než já, tak posloužím aspoň tím odkazem. ![]()
1x
Reciproká rovnice I. druhu a 5. stupně, převedeme na 4. stupeň a to vydělením (x + 1) jeden kořen je x = -1 a dostaneme
3x(4) - 10x(3) + 15x(2) - 10x + 3 = 0
dále vydělíme x(2) provedeme substituci y = x + 1/x
vyřešíme kvadratickou rovnici
1x
Jakou substituci užíváte? x + 1/x = z? To je dobře; nevím, kde máte zádrhal, ale pokusím se to rozšifrovat.
Především, tato substituce tak, jak je, je vhodná pro reciproké rovnice sudého řádu, což není náš případ. Pokud je tohle místo, kde nevíte jak dál, pomoc je snadná: reciproká rovnice (I. druhu) li chého stupně má kořen x = -1 a po vydělení výrazem (x+1) vznikne opět reciproká rovnice, ale už sudého řádu, na kterou lze již příslušná substituce přímo použít ( v našem případě vznikne rovnice 4. řádu 3x^4 - 10x^3 + 15 x^2 - 10x +3).
Tomuhle olasu nerozumím. Nevím, co je zde míněno duplicitou odpovědí, a dělení x^2 jsem neopomněl, já napsal, že rovnice se dá tou substitucí řešit, ale už jsem nerozváděl jak; to jsem si nechal na případné dol´plnění, kdyby problém nebyl v tom snížení řádu, ale v řešení té rovnice sudého řádu.
Jen to, že to samé jsem již napověděl půl hodiny před tím a nějak se mi již nechce provětrávat závity. Ono 45 roků ze školních lavic je již dost.
1x
Náčrtek jsem si stáhl. Mám pocit, že můj scan začíná právě tam, kde ten náčrtek končí. Posílám ho po částech.

A závěr.
Není to jak říkám dopočítáno, ale ten zbytek by neměl být principiální problém, i když početně na tom ještš je dost práce.
A druhý postup výpočtu té odmocniny spočívá v tom, že se odmocňované číslo Z napíše v goniometrickém tvaru Z = |Z|(cos ß + i sinß![]() a úhel beta se rozpůlí.
a úhel beta se rozpůlí.
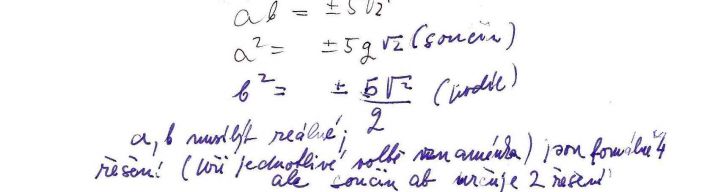
Dobrá práce. To by si měli prohlédnout Ti co se ptají na aritmetický průměr, či jak sestrojit trojúhelník, když mají zadané 3 strany. Aspoň by viděli co je čeká na střední škole. Ovšem pokud je soukromá, tak si jistě poradí jinak a co nezvládnou to hodí na PORADTE. Teď tím nemyslím tazatelku, ta jistě odvedla na příkladu kus své vlastní práce.
doplněno 09.02.10 23:24:Pátrám v paměti. Goniometrický rozklad komplexního čísla, není to Moarova věta?
A tady jsem teď něco našel
doplněno 09.02.10 23:41:Na otázku si odpovím. Není.
Tady je ta mrška věta
A pryč od toho. Začíná mne z toho bolet hlava
No díky, měl bych to umět, takže z mého hlediska to zas takový problém není, i když tohle přímo nedělám, (tedy reciproké rovnice).
Co se týče toho, že autorka dotazu na příkladu odvedla kus práce, s tím mohu jen souhlasit, po zhlédnuti jejího textu (viz výše).
A k tomu goniometrickému tvaru: přímo Moivreova věta to není, ale úzse to spolu souvisí - z ní plyne, že odmocninu dostaneme rozpůlením úhlu beta (v mém zápisu). A pro úplnost druhé řešení dostaneme přičtením čísla pi (jako rozpůlené periody), viz Wikipedie.
Já vím, díval jsem se na její postup již včera. Prakticky, alespoň začátek, jsme měli stejný, jak jsem se mrknul, když asi za 3 hodiny po té co jsem se tím příkladem trochu zabýval, tam hodila to svoje BMP.
doplněno 10.02.10 14:08:Ostatně beru to jako Universitu třetího věku. ČT již vysílá jiné voloviny než "Matematika převážně vážně" a "LAMOHLAV" na internetu před pár lety taky skončil, protože obětavý autor neměl sponzora a musel by provoz serwru hradit ze svého.
Tak jsem shlédla všechny příspěvky a musím říct, že bych nevěřila, že někdo bude tak ochoten pomoct ![]() Chtěla bych tedy poděkovat hlavně Vám a také všem ostatním, kdo se problematikou zabýval.
Chtěla bych tedy poděkovat hlavně Vám a také všem ostatním, kdo se problematikou zabýval.
Jinak, dnes jsem ještě teda byla za vyučujícím a doporučil metodu převedení diskriminantu na goniometrický tvar. Tak se s tím ještě poperu a musím říct, že tedy dobrovolný referát místo zkoušení se mi asi moc nevyplatil ![]()
![]()
Není zač, baví mne to.
Vyjádření diskriminantu v goniometrickém tvaru je rzhodně elegantnější než poněkud toporný postup přes aritmetický tvar a soustavu kvadratických rovnic, navíc je vhodný obecněji pro rešení binomické rovnice x^n ± 1 = 0. Požaduje ovšem trochu větší aparát (goniometrické funkce, Moivreovu poučku. Ale to jistě zvládneš; nějaké odkazy k tomu tam už jsou a kdyby byl nějaký problém, ozvi se.
Jinak pokud vám některá z těch odpovvědí (nejen moje) pomohla, mohla byste možná ji ohodnotit - kliknout na "dobrá odpověď".
Přeji úspěch
doplněno 12.02.10 11:19:Jinak já si nemyslím že se to nevyplatilo. Sice s tím bylo/bude více práce, ale přinese to více znalostí lépe upevněných ![]()
0x
Jak vidím, mezi tím se leccos vyjasnilo a jediný zádrhel pro Vás je, že kořeny vyjdou komplexní; to ale není na závadu, obo C je právě obor komplexních čísel.
Ostatně i kdybychom měli rovnici řešit v oboru reálných čísel, nic by se nedělo, jen by řešení (různé od +1) neexistovalo.
Anebo jse´m přehlédl, že komplexní vyjdou ta z a vy je neumíte odmocnit? Mrknu a když tak ještě napíšu.
doplněno 09.02.10 19:58:Mrknul jsem se a nevím; prostě si to dopočtu a ozvu se zas.
Přesně tak, nejdříve vydělím a na rovnici 3x^4 - 10x^3 15 x^2 - 10x 3=0 použiju substituci, rovnici dám do tvaru: 3(x^2 1/x^2)-10(x 1/x) 15=0 zde subs.: x 1/x=y to celé ^2 a máme x^2 1/x^2=y^2-2.. a pokud pak dosadím tak mám 3y^2-10y 9=0 zde je záporný diskriminant a po dosazení : x 1/x=(-b (-) D^(1/2) )/*a už nevím jak dál s tou imaginární částí. Popř mohu naskenovat nástin, jak jsem řešila a kde tam mám ten problém.
Dobře, ale po v Midsomeru
doplněno 09.02.10 21:16:Tedy já to nascanuju, ty můžeš hned
doplněno 09.02.10 21:18:a já se na to po TV mrknu
No tak tady je prvni část výpočtu odmocniny z komplexního čísla. Ten výpočet není dopočítán až do numerických výsledků, ale to by už neměl ýt problém, a samozřejmě, sliuji dvě metody a na scanu je jedna z nich.
doplněno 09.02.10 22:28:A koukám, že to není nejlépe čitelné, já to ještě rpzdělím na části, aby obrázek byl větší

Jo, tak to fungovalo, stáhl jsem si a to, co tam píšete, je dobře. Co dál, do jsem vystavil níže už včera, je vidět, že jste na příkladu pracovala a o pomoc jste vlala až když už jste opravdu nevěděla; doufám, že Vám můj text pomohl. Pokud by bylo ještě něco nejasné, tak to napište, zkusím doplnit. Kdybyste byla registrovaná, mohla byste použít i interní poštu.
A proč se Vám nedařilo umístit sem obrázek přímo, bude možná tím, že je to rastrový obrázek a to asi systém nepodporuje. Převedl jsem ho na JPG a zkusím ho přidat k této odpovědi. Pokud ani to nevyjde, no kdo chce, může si ho stáhnout.

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.