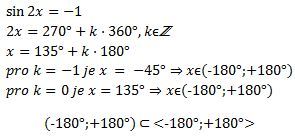Nejste přihlášen/a.
Dobrý den, prosím potřeboval bych poradit, jaké bude řešení pro goniometrickou rovnici
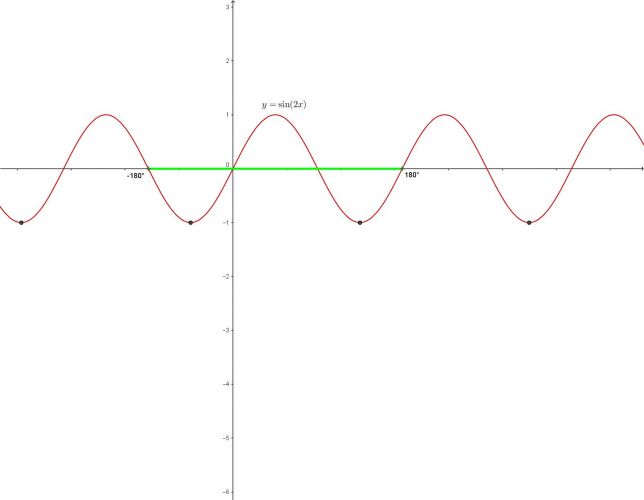
sin2x = -1 s omezením pro x <-180°; + 180°>. A pak za druhé s omezením x (-180°; + 180°).
Mě zajímá jak se bude lišit výsledek když jednou je podmínka <-180°; + 180°> a po druhé (-180°; + 180°).
Díky. A co ještě znamená to ležatý účko. Ale u nějakého jiného zadání by se mohli lišit výsledky, když jednou bude (-180°; +180°) a po druhé <-180°; 180°>? A co ještě znamená to pro k = ... a jak se na to přislo?
To ležaté U je znak inkluze, to znamená je částí (je podmnožinou).
Interval (-180°; +180°) neobsahuje krajní body –180° a 180°.
Interval <-180°; +180°>na rozdíl od předchozího intervalu obsahuje krajní body –180° a 180°.
Uvedená rovnice má nekonečně mnoho řešení. Jednotlivá řešení získáme, dosadíme-li postupně za k celé číslo.
Díky. Už to trošku začínám chápat.
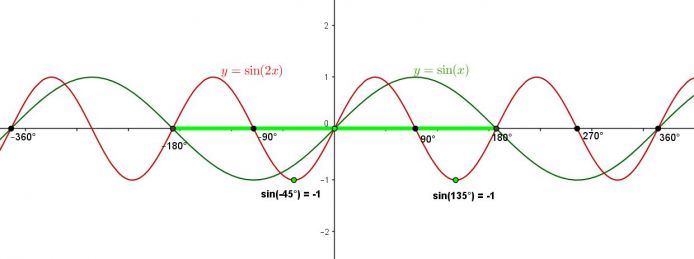
A jak vím že za k mám dosadit jednou 0 a podruhé -1 a ne jiná čísla?
A jak se přišlo početně na to že za k pro -1 vyjde -45°?
Prosím vysvětlil bys mi to.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.