Nejste přihlášen/a.
Zdravím, tak jsem vyřešil jeden příklad 3x a pokaždé jiný výsledek. Pokusy mám označeny v kroužku
1. pokus - jmenovatel jsem nechal tak jak je, porovnal koeficienty, vypočítal A,B,C zintegroval
2. pokus - jmenovatel jsm upravil a dále metodou dosazování mi vyšlo A, B, C
3. pokus - místo dosazování, jsem to všechno roznásobil a porovnal koeficienty.
Co je teda dobře?
Když mám ve jmenovateli 2x-1 mohu to takhle předělat na x-0,5 či naopak?


2x
1. pokus je správně.
Ve 2. integrujete již trochu jiný příklad. Ve jmenovateli jste vytknul z každé závorky 2, takže celkem 2⋅2⋅2 = 8 a ta 8 se někam ztratila. Jinak by byl příklad správně řešen.
Ve 3. pokusu jste zřejmě chybně vypočítal A, B, C.
Obrázky jsou málo zřetelné. Chtělo by to větší rozlišení.
2x – 1 ≠ x – ½ nýbrž 2x – 1 = 2(x – ½)
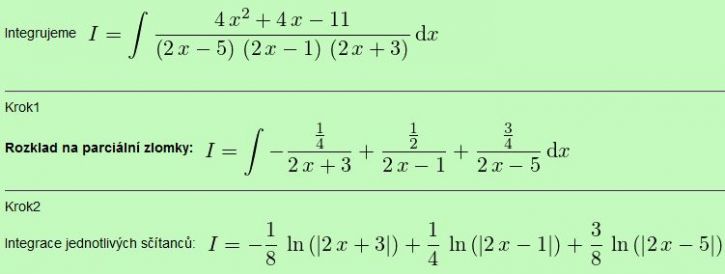
Zase jsem narazil na takový problém.
U tohoto integrálu
1) u jedničky newím jestli je ten rozklad na parciální zlomky dobře, ale B,C = 0 takže vyjde 0 takže budu integrovat jen první a poslední zlomek?
2) zde po dosazení a zintegrování vyšlo podle výsledků
Jde mi o to, že v jednom příkladě, kde mám ve jmenovateli x*(x-4)3 to mám rozložený na A/x + B/ x-4 + C/ (x-4)2 + D/(x-4)3
Proč se to dělá teda na ty 4 zlomky, když mi to vyšlo i s těmi dvěma?
A kdy se dává do čitatele Cx+D?
Díky za odpověd

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.