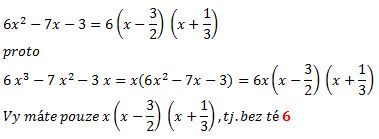Nejste přihlášen/a.
Zdravím, vypočítal jsem integrál (dx/ 6x3-7x2-3x) a nahoře je , co mi vyšlo a dole, co je ve výsledkách. Je to to samé?
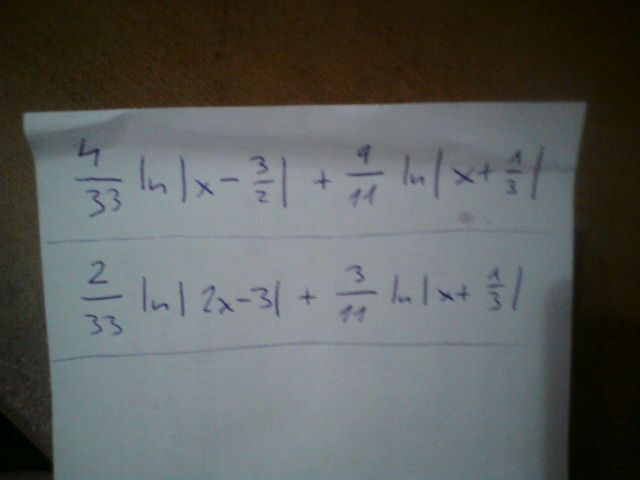
Jak tady uvádíte rozklad na parciální zlomky, tak, já na začátku vytknul x, poté přes diskriminant rozložil na součin
x*(x - 3/2)*(x + 1/3)
Když ty parciánlí zlomky nechám v tomhle tvaru ( A/(x-3/2) ) a budu počítat metodou x= 3/2 atd a dopočítavat A,B,C
A nebo když to třeba upravím na A(2x-3) ... všechno roznásobím a porovnám koeficienty, tak mi A, B, C vyjdou jiné ne?
Ještě pro doplnění jsem znovu napsal
Zda mám ve jmenovateli v závorce nechat ty zlomky nebo upravit na 2x-3 ...
Pokud nechám takhle a nebudu to dále roznásobovat a dám x = 3/2 x=0 x= 1/3 tak vypočítám A, B, C
Kde dělám chybu?
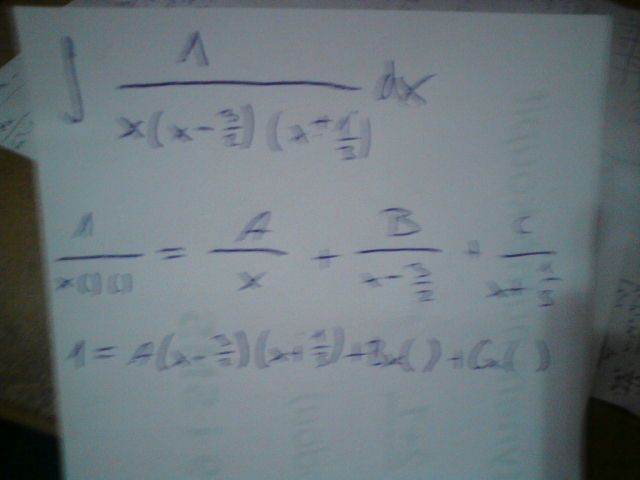
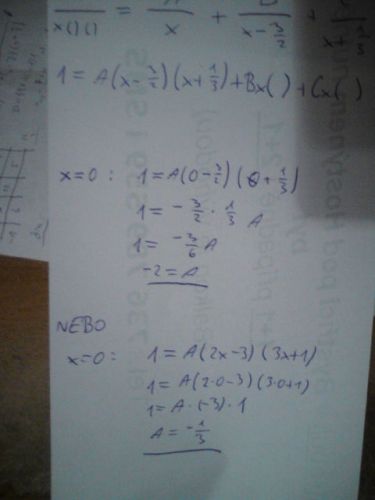
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.