Ahoj,
právě tak trochu koukám na matematiku, probírám diferenciální rovnice, a došel jsem k označení f(x,y) , doposud jsem se s tímto označením nikde nesetkal. Moje podezření je to, že f(x,y) je označení vlastně pro funkci y=f(x) ...Mohl by mi to někdo potvrdit?, Díky moc
2x
Obecně jde o funkci dvou proměnných x,y (kde y může být y(x)). Ale v oboru diferenciálních rovnic se tím rozumí obvykle tvar f(x,y(x))=0. Případně f(x,y(x),yAPOSTROF!(x))=0.
A pozor. f(x,y)=0 a y(x) jsou 2 různé věci. To první dává kompletní informaci o diferenciální rovnici včetně sady řešení, ale to druhé je už je jen funkce, která splňuje první rovnici, tedy řešení (s příšlušnými konstanami).
Zatímco f(x,y,y,yAPOSTROF!...) je zadáno, tak funkce nemusí být ani vyjádřitelná analyticky (může to být integrál, nekoečná suma)
0x
funkce se jmenuje f a má dva argumenty. Jeden její argument se jmenuje x a druhý y.
Odtud označení f(x,y).
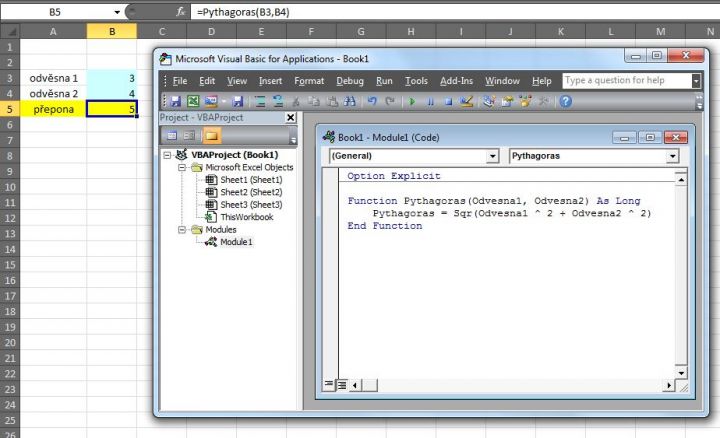
Například pythagorova věta je funkce se dvěma argumenty. Pythagoras(odvěsna1, odvěsna2).
doplněno 08.03.16 07:17:
Jak můžeš vidět na obrázku, Pythagorova věta je funkce dvou proměnných. To co kantoři valí děckám do hlavy, je sám balast.
doplněno 09.03.16 07:13:
a hele. Mému prvnímu doplňku chybí začátek. Admine. Jak je to s tou cenzurou?
Pythagorova věta samozřejmě není funkce, věta je tvrzení, funkce je předpis.
Můžeme říci, že Pythagorova věta určuje (popisuje, vyjadřuje, umožňuje vypočitat) přeponu pravoúhlého troúheůníka jako funkci jeho odvěsen (případně odvěsnu jako funkci přepony a druhé odvěsny). Takže souvislost zde najdeme, ale jsou to různé věci.j
doplněno 07.03.16 19:56: Možná bzch to pro nematematikz mohl trochu royvést."Věta" je pojem matematické logiky. Může mít podobu implikace (když... pak) a její platnost dokazujeme z jiných vět, z definicí a z axiomů. Její soušástí jsou předpoklady, z nichž má záver vyplynout. NNapříklad Pythagorova věta bývá často formulovánaa² + b²=c²ale to není dobře. Správná formulace je třeba:Jsou-li a, b, c délky stran pravoúhlého trojúhelníku, přičemř c je nejdelší /nazýváme ji přepova), pak pro ně platí výše zmíněný vztah.Definice má formálně podobu věty, rozdíl je v tom, že ji nedokazujeme, definuje oznašení nějak=ého pojmu a je tedy "platné z definide"Příklady: třeba tvrzení, že funkce ex je na celé reálné ose rovna součtu svého Taylorova rozvoje, můžeme chápad jako větu (pak alůe musíme vědět odjinut, co je to exponenciální funkce a tuto větu dokazujeme), ale příslušnou teorii lze budovat i tak, že příslušné trvrzení budeme chápat jako definici, pak ale musíme dokazovat to, co jsme při jiném přístupu pokládali za definici.Funkce, to je speciální případ zobrazení a aniž bych zacházel do detailů, mohu ji popsat jako předpis, který každému prvku nějaké mnořiny (množiny vzorů) přiřazuje právě jednu hodnotu z druho množiny "množiny obrazů". Pokud množina vzorů je množina reálných čísel nebo její podmnožina a totéž platí pro množinu vzorů, mluvíme o jedné reálné funkci (jedné) reálné proměnné. Takovou funkci pak značíme třeba f, a "obraz" y, příslušný nějakému konkrétnímu vzoru x, nazýváme hodnotou funkce f v bodě x a píčemey = f(x). Takže bychom měli vlastné důzledně rozlišovat mezi funkcí (rozuměj předpisem) f a její hodnotou f(x), ale ono by to často vedlo k těžkopádnému vyjadřování a tak běžne mluvíme o funkci f(x), respektive o funkci y, ono to sice není korektní, ale nebezpečí nedorozumění snad nehrozí.Jestliže pak mnočina vzorů je tvořena dvojicemi (trojicemi...) reálných čísel (matematik řekne, že je podmnožinou kartézského součinu několika exemplářů reálné osy), mluvíme o (jedné reálné) funkci dvou či více reálných proměnných a píšeme třeba z = f(x,y). Obecně můžeme funkci značit celkem jak nás napadne, třeba f, g, nebo jiným pïásmenem. Je ale řada funkcí často používaných, pro které se ujalo nějaké ustálené zněčení, třeba logaritmus log, přirozený logaritmus ln, ve vyšší matematice známe funkci jedné proměnné zvanou Gama funkce y = Γ(x), funkce dvou proměnných Beta funkce y = B/s,t) a ředa dalších. Figurek používá funkci s označením Pythagoras: přepona = Pythagoras(odvěsna1, odvěsna2). danou předpisem c = Pythagoras(a,b) (a²+b²) ½, což je funkce která díky Pythagorově vědě po dosazení odvěsen pravoůhlého trojúhelníka vrátí jeho přeponu, ale opravdu to není Pythagorova věta. Prostě věta a funkce jsou dva rozdílné pojmy.
doplněno 07.03.16 20:31:
Omlouvám se, je tam hodně přepisů a ještě to zručilo odstavce a pod, snad to pochopíte. Bohužel na tohle nejde použít opravy ale pokud na tom bude někdo trvat, tak to přepíšu.
Četl jste vůbec , co jsem napsal? Proboha, neblbněte tomu chudákovi hlavu. Pythagorova věta NENÍ a nikdy nebyla funkce. Váš obrázek ukazuje ... ale co bych se namáhal, snad jsem to napsal dost jasně. Vy to stejně neuznáte. A ano, nahlásil jsem váš příspěvek. Byl nesmyslný, mimo mísu a urážlivý.
Nicméně, kde na vašem obrázku padlo jediné slovo o Pythagorově větě?
A hlavně odmítá pochopit, co je to věta. Ono už je jedno, jestli "Pythagoras" je pojmenování nějaké klasické funkce nebo klíčové slovo, rozhodně to není Pythagorova věta.
Ad
doplněno 09.03.16 07:13:
a hele. Mému prvnímu doplňku chybí začátek. Admine. Jak je to s tou cenzurou?
Jaký začátek? To je samozřjmeě věc mezi Vámi a adminem, ale trochu by mne to zajímalo, já mám takový pocit, že v této podobě zde byl od začátku. Na druhou stranu postrádám odpověď na můj dotaz "Nicméně, kde na vašem obrázku padlo jediné slovo o Pythagorově větě?" Přehlédl jsem něco?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.