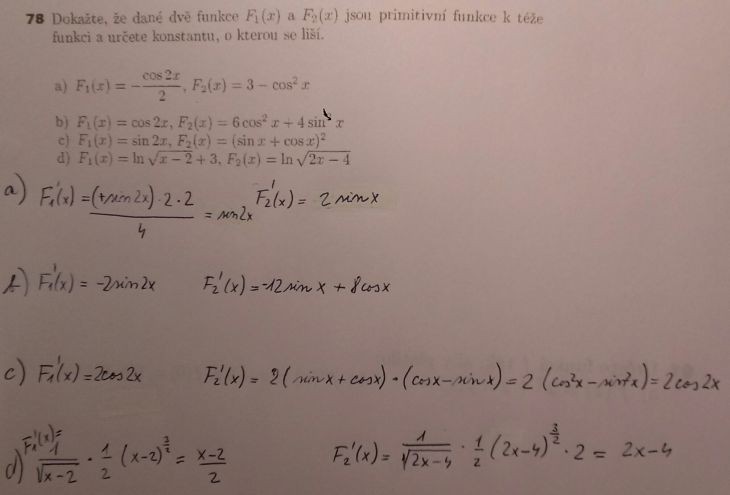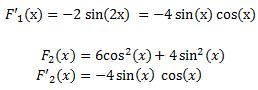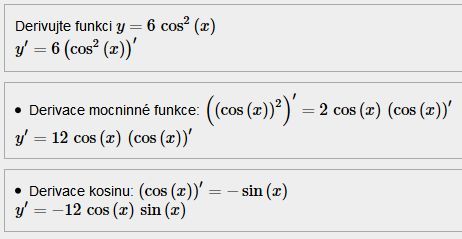Dobrý den, kde dělám prosím chyby?
a) obě se mají rovnat sin2x - druhá mi nevyšla
b) druhá mi nevyšla
c) jejich rozdíl má být 1
d) obě se mají rovnat 1/(2x-4)
Mockrát děkuji
V příkladu c žádnou chybu nevidím, proč myslíte, že to máte špatně?
V příkladu d derivujete (2x −4)½ jako ½*(2x −4)½+1*2 (u F2, u F1 děláte podobnou chybu), má samozřejmě být
½*(2x −4)½-1*2.
Najít rozdíl těch dvou funkcí jistě umíte, jen to sem nepíšete.
(A taková rada na průběžnou kontrolu: primitivní funkce je definována pro x větší než dvě a závěreřná podoba derivace žádnou takovou podmínku neobsahuje; to by vás mělo nastražit.)
No to ano, ale stejné funkce jsou ty derivace, funkce F1 a F2 (primitivní funkce) jsou (mohou být) různé, ale liší se o konstantu. A tu konctantu máte najít; nejsnáze tak, že do obou funkcí dosadíte jeden konkrétní bod. Třeba f tom prvním příkladě a bych dosadil nulu a vyšlo by mi
F1(0) = −½, F2 (0) = 2
a tedy F1(0) −F2(0) = −5/2
a podle věty "libovolné dvě funkce, které mají na nějakém intervalu stejnou derivaci, jsou si na tomto intervalu rovny až na aditivní konstantu
platí i
F1(x) −F2(x) ≡ −5/2 na celé reálné ose
(Ale možná, že by bylo vhodné tohle ověřit přímo, asi takhůe
F1(x) = ½(sin ²x − cos² x) = ½(1 − cos ²x − cos² x) atd.
Prostě proto, že tyhle příklady jsou možná myšleny jako ilustrace obecné věty.)
Mockrát děkuji.
V d) jsem dosazovala za x 3.
Vychází mi to ln (2)1/2+3 a ve výsledcích je ln (2)1/2-3.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.