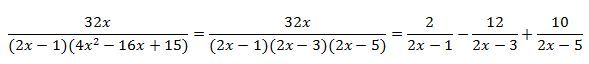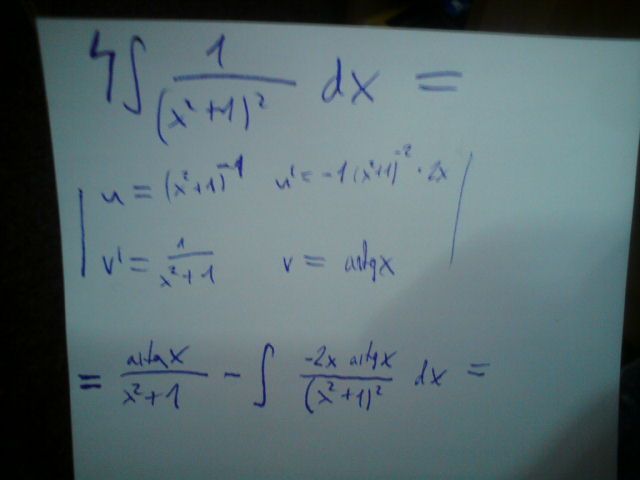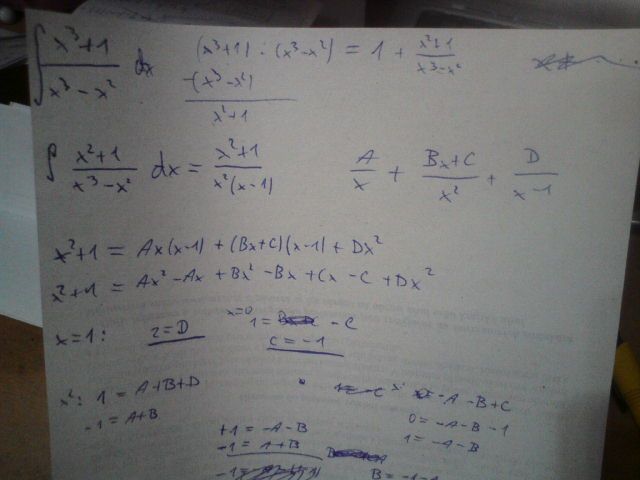Zdravím, potřeboval bych poradit. Má být ta 4 ve jmenovateli? Kd\ž jsem to rozdělil na 3 zlomky, tak mi to vyšlo, kromě toho prvního (A)

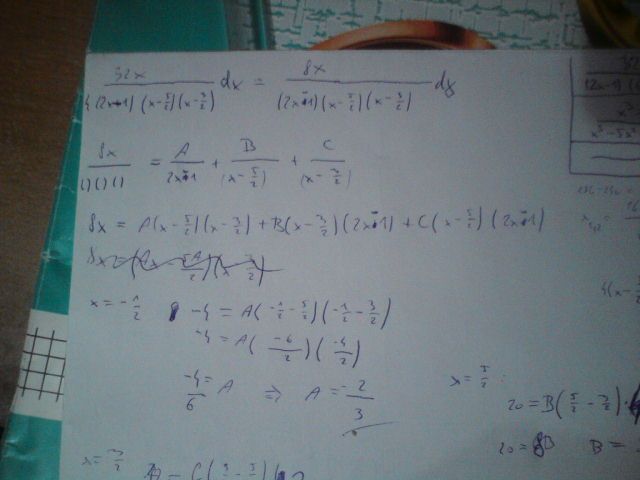
3x
Trochu mám potíře to přečíst (kvůli mým očím, ne kvůli nečitelnosti zápisu), ale vidím-li dobře, rozdělil jste to na mj. dva zlomky se jmenovatelem (x − ½5), jeden má v čitateli B, druhý C. Takhle to dělat nejde, ty dva zlomky dohromady po sečtení utvoří jediný zlomek s tímtéž jmenovatelem a s čitatelem B+C. Už z toho vidíte, že konstanty B, C prostě nelze jednoznačně určit, a při podrobné kontrole (kterou jsem neprováděl právě kvůli "čtecí náročnosti", ale ani nemusím, protože od toho okamžiku už počítáte s nesprávným rozkladem) byste zjistil, že je nedokážete určit ani nejednoznačně, takhle to prostě rozložit nejde. Navíc tam, pokud dobře vidím, nemá být (x − ½5), ale (x − 2), a možná ani to ne?, ale pro zjednodušení se bydu v dalším tvářt, jako by to bylo v pořídku, čili budu se zabývat tím výrazem, kterým začíná vače řešení.
Jeztliže máte ve jmenovateli druhou mocninu kořenového činitele (tedy jedná-li se o dvojnásobný kořen; analogicky to bude i při vyšší násobnosti); v našem případě tedy (x − ½5)², pak tomuto kořenovému činiteli odpovídají skutečně dva parciální zlomky, jeden s jmenovatelem (x − ½5) a čitatelem třeba B (označení je na vás), ale ten druhý, s čitatelem třeba C, ale se jmenovatelem (x − ½5)². Zkuste to tedy znovu s tímto rozkladem.
doplněno 03.03.16 13:18:
Podíval jsem se na to pořádně a vidím, že jsem to skutečně četl špatně. To, co jsem psal, se týká špatně přečteného textu. Nezbyde mi, abych to přeci jenom přepočetl celé, ale dá mi to práci, Tak pardon.
U tohoto příkladu musím jmenovatel roznásobit, a celé pak vydělit? Dostanu 6x-12+ zlomek, který budu dále řešit rozkladem na parciální zlomky?
Nemohu tedy hned jmenovatel upravit na (x+2)*(x+1)*(x-1) a rozkládat na parciální zlomky že?
Když jsem dělil, vyšlo mi to stejně, akorát ještě 3x2 -12x
Na fotce jsem to to zkusil nedělit, ale to 3x2 -12x mi tam chybí.
V čem dělám chybu?

Tato funkce není ryze lomenou racionální funkcí, jelikož stupeň mnohočlenu v čitateli je větší než stupeň mnohočlenu ve jmenovateli. Takže je zapotřebí funkci upravit na tvar:
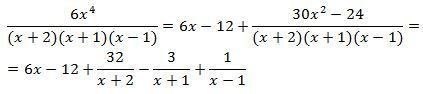
Díky za ujasnění. Jinak integrál (4-2x) / (x2+1)2 dx
Newím si rady, zkusil jsem rozložit na (Ax+B) / x2+1 + (Cx+D) / x2+1
A=0 B=0 C=-2 D=4 mi vyšlo a tím zase ten původní zlomek ![]()
Nebo rozložit na dva zlomky? 4/ (x2+1)2 - 2x/ (x2+1)2
Integrál toho druhého jsem udělal, ale ten první zlomek newím jak.
Po tom rozložení na dva zlomky si ulehčíte – zbavíte se toho druhého zlomku substitucí (2x je derivace x²). A s tím prvním zlomkem si poradite per partes takovým nečekaným trikem. Kdybyste ucělal per parttes na ten zlomek tak, jak je, tak byste si to komplikoval mocnina ve jmenovateli by stoupala. Tak to udělejte opačne. Zlomek 1/(x²+1) integrovat umíte, a když použijete per partes na tento zlomek, tak z něj nakonec vyjádříte ten hledaný. (Ne hned, ještě je na tom potřeba zapracovat, ale měl byste to zvládnout.)
No to právě ne. To perpartesení musíte začít s tím známým integrálem, tedy (zas jsem zapoměl, jak napsat integčítko, tak ho nahradím velkým S)
adrctg x = S dx/(x²+1¨) =
per partes u = 1/(x²+1), u’ = 2x/(x²+1),
v’ =1, v = x
= x*/(x²+1) − S (2x² dx)/(x²+1)² = x*/(x²+1) − S [(2x² +2)dx]/(x²+1)² + S( 2dx)/(x²+1)²
a dostanete rovnici, ve které znáte vše krom toho integrálu, který hledáte, takže ho z ní můžete vyjádřit.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.