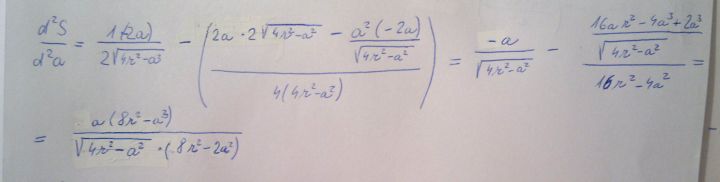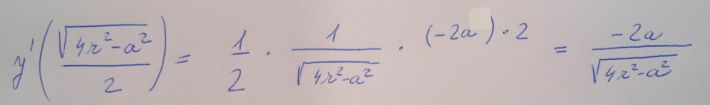Užití diferenciálního počtu

Takhle z hlavy to nezkontroluji,musím si to přepočítat, ale nemůže to být dobře; tak, jak vám to vyšlo, by zápornost závisela na r a to by být nemělo.

Jistě, je to špatně. Hned v prvním členu té druhé derivace jste špatně zderivovala vnitřní funkci, to pod odmozninou, takže ve jmenovateli bude ta odmocnina,tak jak ji tam máte, násobená dvěma, ale v čitateli bude mínus a. Podobnou chuybu máte ve druhém členu. ale to už si pořešíte sama.

To je lepší. ale ještě to není úpln+ě dobře. V čitateli prvního výrazu bude jenm –a a me –2a; nebo chcete-li. bude tam –2a. ale ve jmenovateli bude 4 a to se zkrátí.

A ještě drobná finta: vy hledáte maximum výrazu a*b. Ale je-li maximální tento výraz, je maximální i jeho čtverec a²b², ve kterém už žádné odmocniny nejsou.

Zase zítra

V tom posledním jste násobila dvěma místo půlkou; druhá odmocnina z výrazu A je A na jednu polovinu.

Zkusím probrat ten příklad celý, on je řešitelný mnoha způsoby a popravdě ten váš, jakkoli pravděpodobně očekávaný v rámci užití diferenciálního počtu, je ten nejsložitější, jaký si dovedu představit.

Takže zadání je "do půlkruhu o poloměru r vepište pravoúhelník o maximálním obsahu"; k tomu jste namalovala dobrý obrázek, v němý jste délku základny označila a, výšku b. Vztahy, které dále používáte, jsou :

obsah S = ab,

vztah mezi stranami: r² = (½a)² + b² (Pythagorova věta).

Tyto vztahy jsou samozřejmě vpořádku a budeme z nich vycházet. Hledáme maximum S při podmínce, že a, b splňují uvedený vztah.

Jak jsem už napsal, první ulehčení dosáhneme, když si uvědomíme že je-li maximální (kladný) výraz S, je maximální i výraz S² a naopak zase. Tím se zbavíme nutnosti odmocňovat.

Dále, k vyhledání maxima S vůbec nepotřebujeme derivovat. Lze použít známou nerovnost mezi aritmetickým a geometrickám průměrem, která říká: jsou-li u,v nezáporná realná čísla a označíme-li s = ½(u+v) jejich aritmetický průměr a g: g²=ú*v jejich průměr geometrický, pak vždy platí

s ≥ g

a rovnost nastává právě tehdy, je-li u = v. A jak tuto větu využiji:

Upravím S takto

S = ab = 2(½a)*b = 2g

S² = 4(½a)²*b² = 4g²

kde, že g je je geometrický průměr čísel (½a)² a b², jejchž aritmetický průměr je 2s = (½a)²+b² = r².

Závěr: S ≤ 2r², rovnost čili maximum) nastává pro (½a)²=b². odkud b = r*(½2^½), a = r*(2^½)

Tak to je první způsob, další uvedu samostatně, abych jednu odpověď moc nepřetížil.

Je mi jasné, že postup, který volíte, je véce méně očekávaný, jen jsem chtěl rozebrat všechny možnosti. A teď jen k té poslední derivaci. Rozumím dobře, že derivujete výraz z = ½(4r²–a²)^½ podle a? Pak je postup takto:

z´ = ½* {½[(4r²–a²)^(−½)]*(4r²–a²)´} = ½* {½[(4r²–a²)^(−½)]*(–2a)} =

= – ½a/ {(4r²–a²)^½} = –a/ {2(4r²–a²)^½} .

Je to tak srozumitelné, nebo to mám nascanovat jako obrázek?

Tohle asi je dobrý výpočet, pokud jsem něco nepřehlédl.

Jiíná věc je to, že druhou derivaci počítáte zbytečně a ten výsledek vám vlastně k ničemu není. To, že je druhá derivace záporná, znamená, že v příslušném bodě má funkce S = S(a) lokální maximum, ale vy hledáte globální maximum. Správný postup je tento:

Funkce S je spojitá na uzavřeném intervalu od nuly do 2r. Podle Weierstrassovy věty nabývá na tomto intervalu svého minima a maxima. Z teorie extrémů plyne, že těhto extrémů nabývá buď v krajním bodě tohoto intervalu, tebo v bodě, v němž není derivovatelná, nebo v bodě, kde je derivace nulová (mluvíme o tzv. podezřelých bodech). Krajní body jsou dva, totiž a = 0 a a = 2r, pro něž platí S = 0, a protože v ostatních bodach je S kladné, je v těchto bodech absolutní minimum funkce S. Derivovatelná je funkce S všude, takže zbývá jediný další podezřlý bod, v němž je první derivace nulová a v něm tedy prostě musí být globální maximum.

Pokud neznáte Weierstrassovu větu o extrémech spojité funkce, můčete použít tento postup: vyšetříte znaménko první derivace. Zjistíte, že vlevo od stacionárního bodu (tj. bodu nulové derivace) je první derivace kladná a S je tam rostoucí, vpravo od něj je záporná a S je klesající, odkud také plyne, že ve stacionárním bodě nabývá svého maxima. Q.E.D.

Proč by a nemohlo být větší než r? Ono a je dvojnásobek b, "rozkládá se" ma obě strany od počátku.

A jen znova upozorňuji, že výpočet druhé derivace do řešení tohoto příkladu prostě nepatří.

Pomocí druhé derivace se ověřuje lokální extrém. Znáte rozdíl mezi lokálním a globálním extrémem? Pak jistě víte, že hledání globálních extrémů se dělá přeci jenom poněkud jinak, i když s využitím technik "lokálních".

Jinak je samozřejmě pravda, že pokud globální maximum leží uvnitř intervalu, je to zároveň lokální maximum a tak v něm bude první derivace nulová (tedy pokud existuje) a druhá derivacezáporná. Ale pro nalezení globálního maxima je potřeba především vědět, že existuje. A když to vím, že existuje, tak ověření znamémka druhé derivace je zbytečné.

Učili jste se, jak se hledají globální extrémy? Tak mi řekněte, jak se postupuje při hledání maxima, jestliže ta vyšetřovaná funkce bude slořitější a bude mít tři stacionérní body, a druhá derivace bude záporná ve dvou z nich?

Nebo si představte, že by funkce S byla pro kladné S definovaná tak jako ta vaše, alle S(0) bude rovno 3 485 781 r². Jaké bude maximum téhle funkce?

Vy se učíte jednodušší příklady, ale určit+ě jste se učili i o rozdílu mezi lokálním a globálním extrémem. A výše uvedené příklady by vás měly přesvědčit, že souvisloast se znaménkem druhé derivace tu je, ale jeho ověřování ke při nejmenším nadbytečné.

Trochu ano. A takhle?

"Takhle vyšlo b a a = r . 2^1/2"

Nebo, ještě lépe,¨

Takhle vyšlo b; a =r. 2^1/2

Tak potom ano. A pak se musíte holt spokojit s tím, že uvedený příklad řešíte ne zcela přesně a spolehnout se na to, že ten výsledek je v pořádku. A vysvětluje se tím to, že můj postup je pro vás zcela neznámý.

Ale monotonii jste se učili? Pokud ano, tak tomu druhému postupu byste měla rozumět.