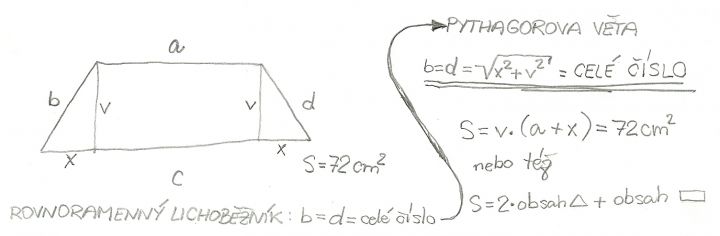Lichoběžník - strany

Úloha je řešitelná jako difantovská rovnice

Označíme - li základny "a" "b" a výšku "v" pak plocha je P=((a+b) /2)*v

v=144/(a+b) můžeme zjistit všechny celočíselné dělitele čísla 144 mezi jinými 36 a 48 a v tom případě bude výška lichoběžníku 4 nebo 3.

Teď již stačí určit délky stran jejichž součet je 36 nebo 48 a rozdíl jejich délek je v prvním případě dvojnásobek čísla 4 to jest 8 a v druhém případě dvojnásobek čísla 3 to jest 6.

Tomuto v prvním případě odpovídají délka základny 21 a 15 a v druhém případě 28 a 20

Ted již stačí jen zkontrolovat, že i ramena mají celočíselnou délku při daném obsahu. Úloha má nejméně dvě řešení.

Tak to bude asi nějaký úkol ze školy, že? Nejlepší je nakreslit si to. Řešení Ti neprozradím, prozradím Ti jen, že úloha řešení má, ale dám Ti návod. Co je rovnoramenný lichoběžník? Obdélník/čtverec + dva stejné trojúhelníky, že? Jak se vypočítá obsah trojúhelníku a obdélníku? Alfa a omega této úlohy je strana "b" = "d", ta musí být po odmocnění celé číslo, když je dáno, že délky stran jsou celá čísla. Strany "a" a "c" už potom vyplynou samy. Pythagorovy trojúhelníky. Co si dosadíš jako délku strany "x" a výšky "v" (celá čísla) na obrázku, abys dostala stranu "b" po odmocnění jako celé číslo? Všechny délky jsou celá čísla, z toho také vycházej. Už je to jasnější?

Upozorňuji, ýe i obdélník je speciální případ rovnoramenného lichoběžníku. A obdélníky, vyhovující zadání, najdeme snadno všechny. Stačí 72 rozdělit na součin dvou celých kladných čísel.