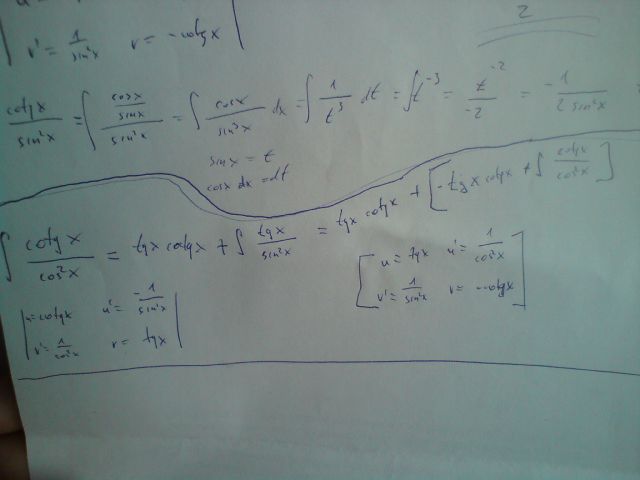Nejste přihlášen/a.
Cs potřeboval bych pomoct s tímto příkladem.
Vyšel mi pokaždé jinak. Moc mi nejde to doplnění na čtverec.Můj postup se liší v tom, jestli tu jedničku mám dát do závorky nebo ne.
U toho prvního mám vše v závorce. u druhého jsem dal jedničku za závorku.


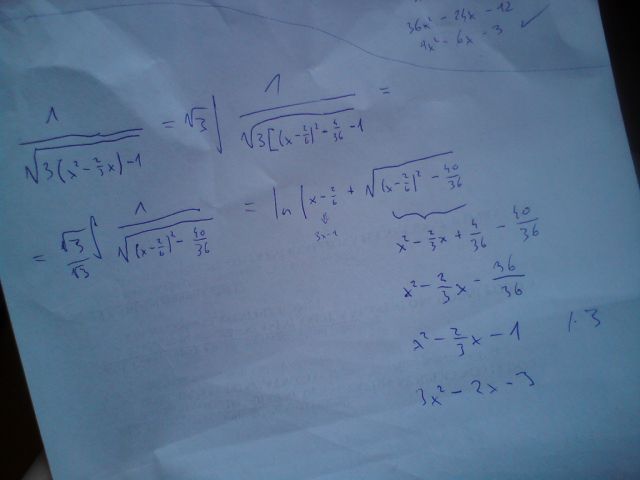
2x
Ten druhý postup je chybný. Trojku musíte vytknout ze všech členů, nikoli jen z prvních dvou a poté ji dát před odmocninu. Ten první potup se zdá být správný. Zlomky bych ale krátil.
doplněno 13.02.16 19:56:
Za konstantu C můžete volit ln 3 + C a výsledek pak upravit:
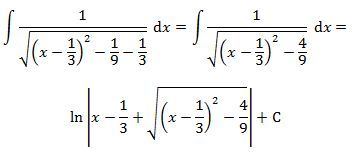
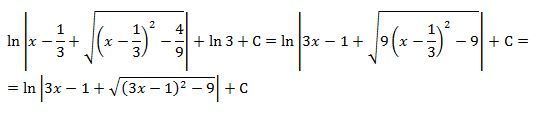
Za konstantu C můžete volit ln 3 + C ...
Protože log x + log 3 = log 3⋅x,
logaritmus součinu rovná se součtu logaritmů jednotlivých činitelů.
Potřeboval bych poradit s tímhle.
Zkusil jsem per partes a vyšlo mi 1/2 * tan²x
Pak tan(x) jsem nahradil sin(x) / cos(x) a vyšlo mi 1/cos^2(x) *1/2
Jak z 1/cos^2(x) *1/2 dostanu to 1/2 * tan²x?
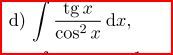
Obě funkce jsou primitivní funkce k funkci tan(x)/cos2(x). Navzájem se liší o nějakou konstantu, v tomto případě o ½ .
Platí věta: Nechť funkce F(x) je primitivní k funkci f(x) na intervalu I. Pak každá jiná
primitivní funkce k funkci f(x) na I má tvar F(x) + c, kde c ∊ R.
Jinými slovy, předchozí věta říká, že známe-li jednu primitivní funkci, známe všechny.
Rozdíl dvou takových primitivních funkcí je na intervalu I konstantní.
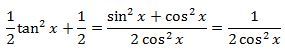
Chybu tam nevidím, pouze tento postup k cíli nevede. cotg(x) nahraďte cos(x)/sin(x) a dál použijte substituci.
0x
Mohu se zeptat, zkušených počtářů, kteří integrují ručně, jaké přesně používají finty ,aby se neztratili v moři susbstitucí a nikdy nikde nic nezapoměli?
Například jestli si to rozvrhnou do více kroků? Někam si to poznamávají? Nějaé ověřování kroků?Nebo jdou na to obráceně, že si vlastně řeknou, že budou počítat integrál z 1/sqrt(x^2-1), ten si pamatují, napíší výsledek a pak začnout výsledek i počáteční výraz ladit, až se dostanou do původního zadání?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.