Nejste přihlášen/a.
Dobrý den, měl bych dotaz na jeden příklad na geometrii. V kótovaném promítaní sestrojte průsečík přímky m= MN s rovinou alfa=ABC. A(-45,-20,10) B(-10,-20,30) C(-40,10,10) M(-30,15,20) N(-25,-20,50). Prosím o pomoc zda by mi někdo poslal vypracovaný výkres i s podrobným postupem. Děkuji Martin
Osu narýsovanou mám všechny souřadnice také jenže nevím jak dál mám postupovat
doplněno 14.01.16 12:03:
Prosím o pomoct
0x
Jedná se o základní konstrukci průsečíku přímky s rovinou.
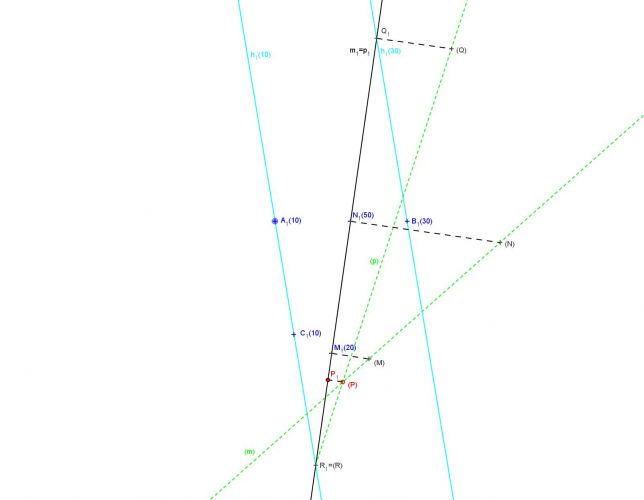
1. Přímkou m = MN proložíme rovinu kolmou k průmětně. Tato rovina protíná rovinu α určenou body A, B, C v přímce p. Průměty přímek splývají. Přímka p (průsečnice promítací roviny s rovinou α) se nazývá krycí přímka přímky m.
2. V rovině α zvolíme dvě hlavní přímky h(10) (tj. přímka AC) a h(30) (tj. přímka procházející bodem B) .
3. Přímku p určíme právě pomocí průsečíků s těmito hlavními přímkami.
4. Promítací rovinu sklopíme do hlavní roviny o kótě 10; ve sklopení najdeme (P) = (m)⋅(p) a zpětným otočením sestrojíme P1.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.