3x
Z obvodu čeho?
Největší moýný obsah vyjde, když se bude jednat o kružnici (Didonina isoperimetrická úloha), ale bez specifikace může vyjít cokoli, co tento obsah nepřesáhne.
No tak čestiúhelník je šest rovnostranných trojúhelníkú, strana je šestina obvodu, vzorec pro výšku je jednoduchý (nabo ho spoštu Pythagorem).
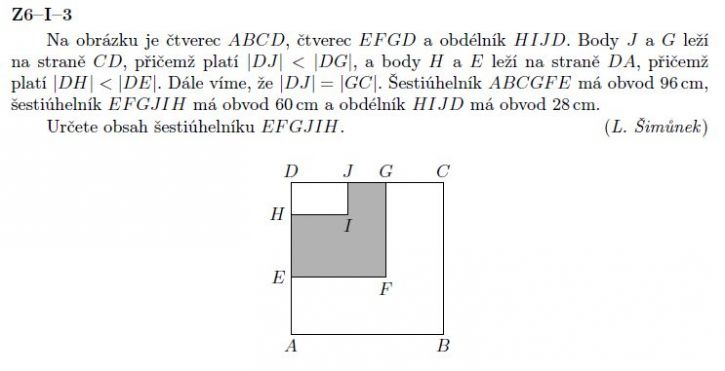
doplněno 07.01.16 18:59: Pokračují =|GC|.Šestiúhelník ABCGFE má obvod 96 cm,šestiúhelník EFGJIH ( o kterén mluvíme)má obvod 60 cm s obdélník HIJD má obvod 28 cm.Určete obsah šestiúhelníku EFGJIH.
doplněno 07.01.16 19:44: A navíc se mi to snaží vysvětit a vy to snad umíte?
Tak red uz by to mohlo jít. Jen se mi zdá, že jste tuhle odpověď opravoval a při tom něco vypadlo. pro jistotu napíšu kousek vašeho teztu a červeně do něj doplním, co si myslím, že vám vypadlo:přičemž platí|DJ| =|GC|,a body H a E leží na straně DA, přičemž platí |DH|
Sakra, taky mi toho spoustu vypadlo, zkusím to napsat znovu, ale později, ono mi tohle dělá šasto.
doplněno 07.01.16 21:39: Dobrý by bylo jestli bychom se dobrali k tomu Řešení a že mi to pomůžete rozluštit do zítřka Děkuji
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.