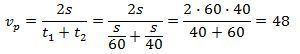Nejste přihlášen/a.
Ahoj potřebovala bych pomoct![]()
Dnes jsme dostali ve škole ukol..:/Nikdo si s ním neví rady:/
jJede autíčko z bodu A do bodu B průměrnou rychlostí 60km/h u bodu B se otočí a jedezpět do bodu A průměrnou rychlostí 40km/h..Zjisti průměr z průměru nebo porovnej oba průměry,ale vysledek nesmí vyjít 50km/h..
Prosím poraďte!![]() Děkuji
Děkuji
4x
Průměrná rychlost se vypočte, když celkovou dráhu vydělíme celkovou dobou jízdy.
Dosadit a vypočítat to snad již není problém.
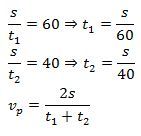
1x
Zas mi to zkurvilo formát. Dám to sem znovu po čáastech.
Část prvá:
Po pravdě sama formulace mi přijde poněkud zmatená. Ano, průměrnou rychlost celé jízdy spočteme podle @x , ale na co se vlastně ptá zadavatel, to je trochu zmateční. Vezmu to od konce:
"výsledek nesmí vyjít 50 km/h"
Co to je? ten výsledek vyjde tak, jak vyjít má, a nikdo nemá co zakazovat nějaký výsledek. Smysl pravděpodobně je upozornění, že výsledek 50 km/h není správný, ale takhle to není matematická formulace.
"Zjisti průměr z průměru nebo porovnej oba průměry"
Co mám porovnat? Jaké oba průměry? Pokud se tím myslí průměrná rychlost "tam" a průměrná rychlost "zpět", tak porovnáním vyjde, že z A do B jelo auto větší průměrnou rychlostí než zpátky, ale pochybuji, že o to zadavateli šlo.
"Zjisti průměr z průměru" patrně má být množné číslo, tedy zjisti průměr z průměrů, ale jaký průměr? A z jakých průměrů?
část druhá:
Známe aritmetický průměr, harmonický průměr, geometrický průměr, a průměrná rychlost je něco ještě jiného. Pokud to pochopím tak, že mám zjistit aritmetický průměr obou průměrných rychlostí, tak by vyšel právě ten "zakázaný" výsledek, ale ono to tak formulováno není. Jen to ukazuje, že jde asi o něco jiného.
Vykašlu se teď na hádání formulace zadání (nezlobte se, ale já si myslím, že si jen myslíte, že jste takhle to zadání dostali, ale že jste slova pana učitele nepochopili a špatně zapsali; opravte mne, jestli se mýlím) a učiním několik poznámek k problému. Snad z toho pochopíme, oč kráčí, ale o elegantní zadání se pokoušet nebudu.
Tak za prvé ty dvě průměrné rychlosti jsou jasné. Těch 60km/h je dráha od A do B, dělená časem, za kterou ji auto ujelo, tak jak to píše @x. V jeho označení je to s/t1, označme si ji v1. Podobně ta druhá průměrná rychlost je s/t2. Označíme ji v2. Pravděpodobně nás bude zajímat průměrná rychlost jízdy tam a zpět, kterou x označil vp, jako v průměrná.
část třetí:
Běžně mnoho lidí napadne, že průměrná rychlost bude aritmetickým průměrem průměrných rychlostí tam a zpět a bude zkoužet
vp =? ½(v1+v2)
jenže to je špatně (ne proto, že to někdo zakázal, ale prostě proto, že správný výsledek, jak spočítal x, je jiný. A jaký? x napsal už konečný výsledek, ale když si to rozmyslíte, přesvědčíte se, že pro průměrnou rychlost platí
1/vp = ½(1/v1+1/v2)
slovy, převrácené hodnota průměrné rychlosti je aritmetickým průměrem převrácených hodnot "průměrovaných" rychlostí, odborně, průměrná rychlost je harmonický průměr rychlostí v1 a v2.
Jinak výpočet té průměrné rychlosti máte uveden výše, ale já mám pocit, že sdtoj vašeho nepochopení je jinde a pokusil jsem se ho odkrýt.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.