Dobrý den, v čem prosím dělám chybu? Výsledek má být: v1=(0;-4), v2=(2.31/2;2)
Mockrát děkuji
v22 = 16 - v12
v22 = 16
|v2| = √16
v2 = ±4
O tom, kde se vylouci to reseni +4 budu muset premyslet.![]() (stejne jako o tom v1 = -2√3)
(stejne jako o tom v1 = -2√3)
Nacrtni si ty vektory do souradnic pro predstavu, jestli ta reseni jsou zhruba spravne (kvadranty, blizkost k ose x nebo y, velikost obecne). [Ano, reseni z ucebnice jsou spravne]
U jednoho znaménka neplatí, že svírá s vektorem u úhel 60°. Musím si to nakreslit? Z výpočtu to nepoznám? Děkuji
Já bych měl připomínku k vzorci pro výpočet cos φ . V čitateli by neměla být absolutní hodnota. Pro úhel, který svírají dva vektory, platí: 0 ≤ φ ≤ 180°, takže cos φ vychází pro úhly větší než 90° záporný.
Druhou souřadnici vektoru v bych raději počítal ze vztahu
½ = (v1∙√3 + v2∙(–1))/(√(v12 + v22 )∙2)
½ = (v1∙√3 + v2∙(–1))/8
a tím se vyhneme těm nadbytečným řešením.
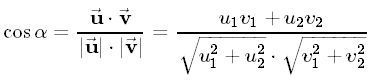
3x
Uvodem upozorním na nepřesnost v tom, jak používáte označení. Vy totiž značení v1, v2 používáte k rozlišení souřadnic vektoru v, kdežto v tom vámi uváněném očekávaném řešení (zřejmě z výsledků v učebnici) jsou takto rozlišeny dva vektory, které oba svírají ten hledaný úhel. Ale s tím jste si celkem poradila, v podstatě při výpočtu "učebnicové" značení prostě ignoruujete a ke kolizi vám nedochásí,.
Takže k vlastnímu řešení: postup uvedl čtenář, který také upozornil na chybný způsob sčítání odmocnin. (Pokud vás zajímá, proč vám přes tuto chybu vyšlo řešení (0,±4), tak to souvisí s tím, že když je jedna souřadnice nulová, nesčítáte dvě odmocniny a chybný postup nemá nárok se projevit). A jak zjisíte, které z řešení je to správné? Vy řešíte rovnici
L = 1/2
kde L je ta levá strana, a v průběhu řešení tuto rovnici umocníte na druhou. Pak se ale nepozná, zda jste řešila rovnici L = 1/2 (šedesát stupňů), nebo rovnici L =&minus 1/2 (stodvacet stupňů). Váš postup najde jedním vrzem oba případy a mezi nimi pak musíte rozlišit tak, že je dosadíte do té původní, neumocněné rovnice.
doplněno 27.12.15 14:20: Oprava, ne L =&minus 1/2, le L =− 1/2
0x
@x a @kartaginec to - ostatne jako vzdy - vyresili mnohem elegantneji a i zjistili, jak se zbavit tech nadbytecnych reseni.
Tim uz o tom nemusim premyslet. Stejne jsem na nic nemohl prijit (krome toho, ze sam bych to vyresil na par radcich vypoctem v polarnich souradnicich hlavne z toho duvodu, ze skalarni soucin jsem od skoly snad nikdy nepouzil a jeho princip, vlastnosti a pouziti si musim pokazde pripomenout ![]() )
)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.

