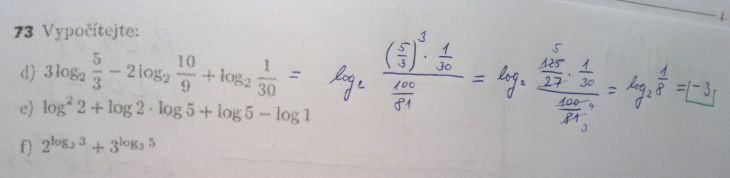Dobrý den, jak se prosím vypočítá e), f)? Mockrát děkuji
3x
f) = 3 + 5 = 8
log pri zakladu "n" a "n na neco" jsou inverzni operace. Vysledkem je ten argument logaritmu.
Neboli jinak: log23 rika, ze hledame takove x, pro ktere 2x je 3. Kdyz ho najdeme, tak ho dosadime do toho 2log23, tedy dostame 2x coz uz ale z drive vime, ze je 3, protoz tak jsme x urcili, aby nam 3 vyslo.
doplněno 28.11.15 19:01:
e) = log2(log2 + log5) +log5 + 0 = log2.log10 + log5 = log2 + log5 = log10 = 1
doplněno 28.11.15 19:02:
Ne + 0, ale -0.
Moc děkuji
Ještě prosím, jak se násobí logaritmy?
Tady byl jeden z čitatelů 1, ale kdyby tam bylo třeba log 3 . log 9? Nebo to se počítá jen na počítačce?
log3.log9 = log3.2.log3 = 2log23
log3 i log9 jsou "oskliva" cisla (deset na kolikatou je 3 nebo 30? Z toho vidis, ze to nebude zadne cele cislo).
Je to log2x posunute o 4 doleva a 1 dolu. Pak je jeste kvuli abs.hodnote udelan obraz podle osy y posunute o ty 4 doleva.
Snad to mam dobre. Co ukazuje Wolfram?
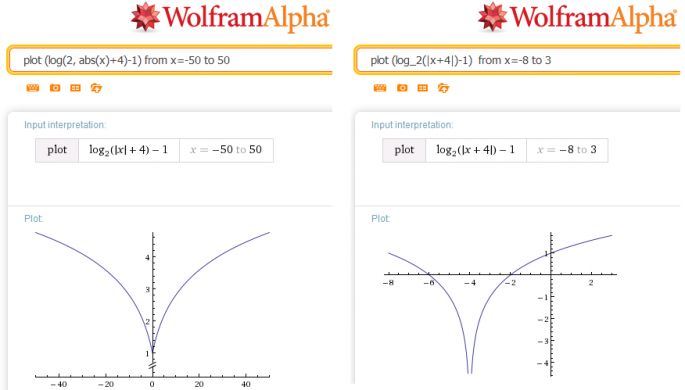
Výsledek viz obrázek.
Děkuji, špatně jsem to šoupala. Takže je stejný postup, jako kdyby byl celý výraz v absolutní hodnotě?
Jen tak další otázka: Jak se prosím dělá v Wolfram dolní exponent?
doplněno 28.11.15 20:46:
Dělala jsem to stejně jako vy, výsledek v učebnici mi přijde, jako by to bylo celé v absolutní hodnotě. Předtím jsem logaritmus překlopila podle y a celé jsem to šoupla.
doplněno 28.11.15 21:01:
Už jsem ten dolní index našla a wolframalpha má stejný výsledek jako je v učebnici
doplněno 28.11.15 21:05:
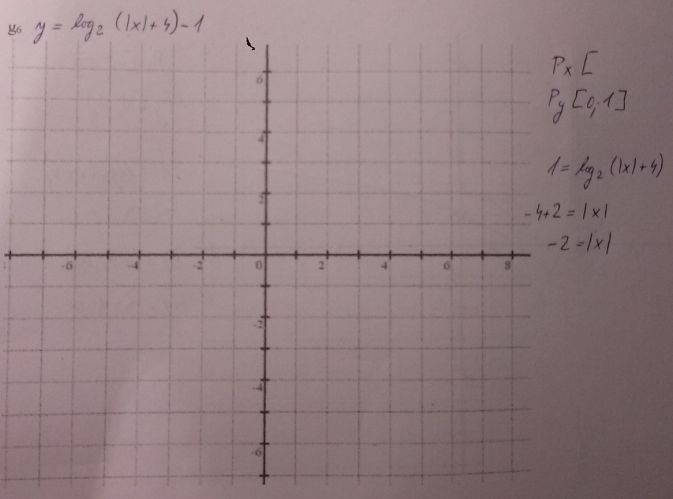
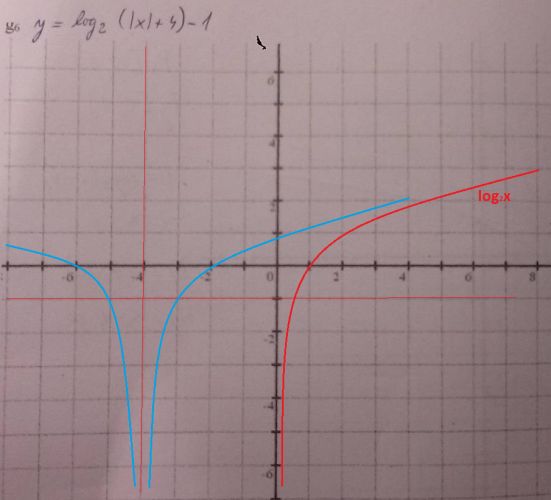
Už jsem si na to vzpomněla, u kvadratické funkce se to vlastně také nejprve šoupe a když je x v absolutní hodnotě, tak se celá funkce překlopí až na závěr.
Děkuji za pomoc
Aha, tak jsem to prece jenom v te rychlosti popletl. Ten posunuty graf se zrcadli podle osy y (a ne te posunute o 4), protoze v abs. hodnote jen jen neposunute x. 
Omlouvam se za matení.
Ciste ze zajmu pro pripadne zajemce jsem oba typy abs.hodnot dal spocitat Wolframu. Grafy jsou spravne.
Jak říká čtenář, log 3 a log 6 jsou "ošklivá/ čísla, ale na druhou stranu "dobře sladění", což umožňuje použít ad hoc postup. který také uvádí, Jinak obecně nějaký zjednodušující vzorec podobný tomu, který převádí součet logaritmů na logaritmus součinu, není.
Ano. lze napsat
(log a)*(log b) =log a^log b, ale tnení moc zjednodušní
Jeste me k tomuto konkretnimu (log3) napadlo nasledujici:
log3 je asi 0,5 (presneji 0,4771...). Lze si to pamatovat, protoze v grafech vykreslenych v logaritmickych osach/ose je 3 (tedy log3) zhruba v pulce mezi 1 a 10 (log1 a log10).
Kvuli vlastnostem logaritmu je i 30 v pulce mezi 10 a 100, 300 v pulce mezi 100 a 1000 atd.
napr.; log 30 = log10.3 = log10 + log3, cili je to porad log3 posunuty na ose grafu o 1.řád doprava. Stejne jde dokazat pro log10 a log100. Vzajemna poloha log1, log3, log10 se tedy nemeni s pribyvajicimi rady a 3000... ( log3000...) bude vzdy v "pulce" (0,47) mezi 1000... (log1000...) a 10000... (log10000...) .
Obdobne dalsi vyznamne body na logaritmicke ose jsou log2 = 0,3 a log5 = 0,7
doplněno 01.12.15 21:39:
Souhlas s @kartaginec v tom, že log5.log7 = log(7log5) neni zjednoduseni.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.