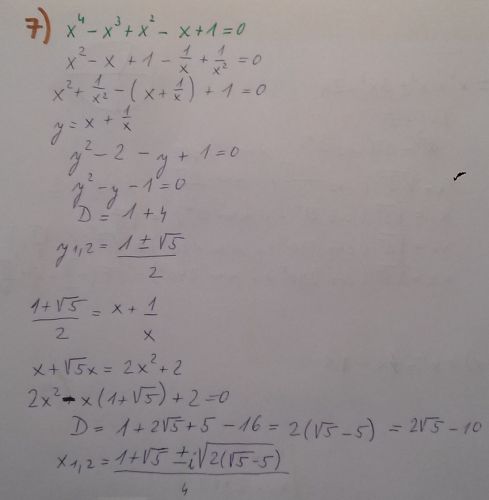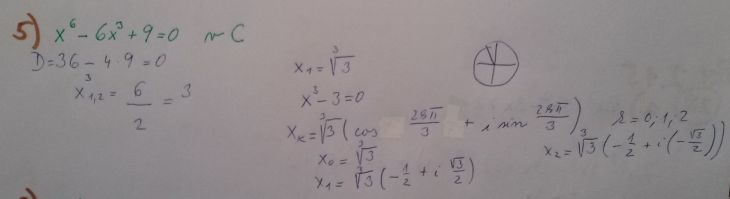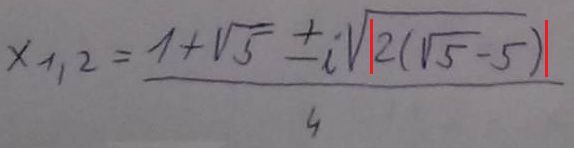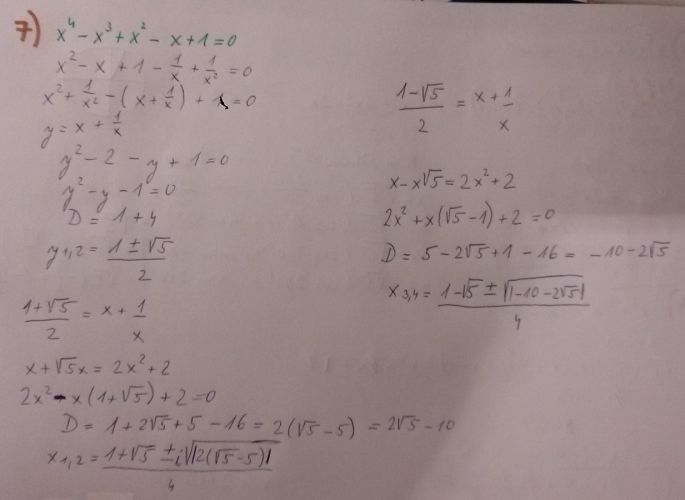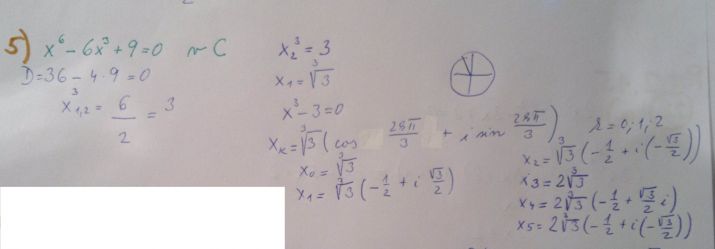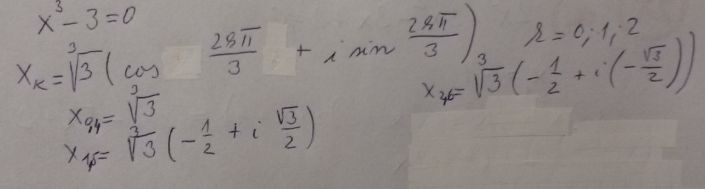Dobrý den, pomohli byste mi prosím s těmito příklady? Mockrát děkuji
doplněno 22.11.15 15:29:
Ten příklad 1) (3. obrázek) je správně, jen se mi zobrazily výsledky na wolframalpha v jiném tvaru.
Děkuji,
7) mám ještě výraz pod odmocninou umocnit a odmocnit, aby se odstranila absolutní hodnota?
1) ten červený výsledek není dobře?
5) jak poznám, že těch kořenů bude 6, když řeším rovnici x3-1, která má kořeny 3?
5) viz kartaginec. Ti vyslo (x1,2)3 = 3 a dale pocitas pro x13 = 3 a uplne jsi zapomnela na x2 (ktere je v tomto pripade stejne x1) takze nemusis pocitat jeho koreny, protoze jsou stejne jako pro x1. Zvysi se tim tak mocnost vsech korenu x1 o jedna, tzn. budou dvojnasobne.
1) vysledek je dobre, jen tam mas napsano x2,3 misto x3,4
7) 2(√5 -5) je asi 2(2-5) = -6
vyslo ti tedy (1/4)[1 + √5 ± √(-6) ], coz je to same jako
(1/4)[1 + √5 ± i. √|-6| ]. To uz nejde dal upravit.
Muzes ale misto 2(√5 -5) to vynasobit -1 (tim vlastne to udelas kladne, stejne jako by udelala absol. hodnota) a dostanes 2(5-√5). Tvar pak bude (1/4)[1 + √5 ± i. √2(5-√5) ]
To je otázka rozkladu na kořenové činitele. Substituce x³= y vede na rovnici y²–6y +9 = 0, y1,2 = (6±D)/2 , D = 0, y1,2 =3±0
a tedy y²–6y +9 = (y−3)*(y−3) =(y−3)²
Z toho vidíte, že y = 3 je´dvojný kořen, příslušný kořenový činitel (y−3) je tam dvakrát a v kažré té závorce řešíte rovnici pro x – x³ = 3. Pokaždé má tři řešení, každé z obou závorek se tedy rozloží na tří kořenové činitele a dohromady jich bude šest.
Dvojnasobny/dvojmocny/dvojny (nebo jak se to jmenuje) koren neznamena ze je je 2x vetsi, ale ze dalsi koren ma stejnou hodnotu jako nejaky uz predesly.
Tedy:
x3 = x0
x4 = x1
x5 = x2
Vsimni si (obr.2), ze ti nejprve vysly 2 treti mocniny korenu, ale dal uz pocitad jen s jednou. Tam se ti ztratila ta dvojnost a proto ti vysly jen 3 koreny, kdyz polynom 6-teho stupne jich ma 6.
Děkuji, takže takhle?
doplněno 24.11.15 07:36:
7) Jak prosím přijdu na tohle?
2(√5 -5) je asi 2(2-5) = -6
Děkuji
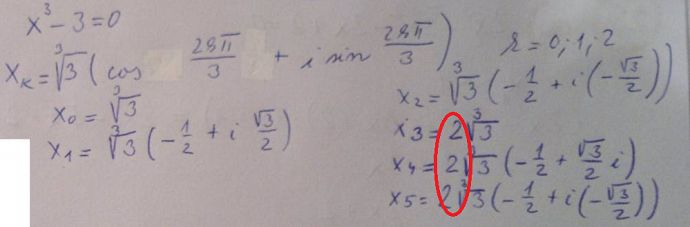
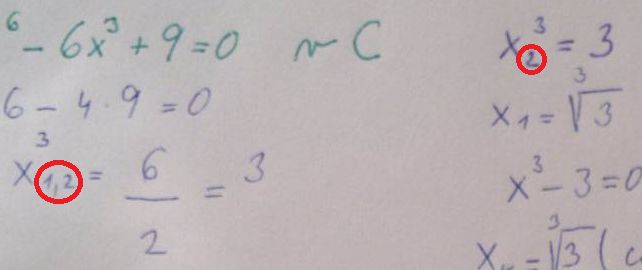
Ted mas ty koreny zapsane dobre.
K √5:
√4 = 2
√9 = 3
5 je mezi 4 a 9, o hodne blize k 4 nez k 9, takze √5 bude mezi 2 a 3, blize k 2 nez 3 (√5 = 2,236...). Take vim, ze 252 = 625, tedy √6,25 = 2,5, tzn. √5 bude mezi 2 a 2,5. Ja do vzorce dosadil 2 (je to cele cislo a proto nemusim pocitat s desetinnymi cisly).
Je to jen pro hruby odhad vysledku v hlave bez kalkulacky. Jde o to zjistit znamenko a pripadne řád, tedy jestli je vysledek +7 nebo -70.
0x
Tak snad něco málo teorie.
ZÁKLADNÍ VĚTA ALGEBRY říká, že každí algebraická rovnice stupně alespoň prvního má v komplexní rovině alespoň jeden kořen.
Tedy pro polynom stupňe n ≥ 0
a0xn + a1xn−1 + ... +an, a0≠0
existuje komplexní číslo x1 takové, že
a0x1n + a1x1n−1 + ... +an = 0.
A protože ten poslední výraz je nulový, vidíme, že
a0xn + a1xn−1 + ... +an = a0xn + a1xn−1 + ... +an −(a0x1n + a1x1n−1 + ... +an )
_____________________
Po této úpravě můžeme pokračovat: dáme dohromady vždy stejné mocniny x a ve výraze ak(xn−k −x1n−k), k = 0,1,...n
vytkneme (x−x1) s použirím vzorečku pro Aj − Bj.
První závěr: každý polynom Pn(x) stupně většího než nula lze převést na tvar (x−x1)*Bn−1 , kde B je polynom stupně o jednu menšího, a výraz (x−x1) je tzv. kořenový činitel.
Tento postup můžeme opakovat tak dlouho, dokud z polynomu B nevznikne polynom stupně nula čili konstanta, a vidíme, že každý polynom lze zapsat jako a0 násobeno součinem právě n kořenových činitelů, z nichž některé mohou být stejné; počet polynomů, které kspu stejné, je násobnost odpovídajícího kořene.
Druhý závěr: Každý polynom stupně n alespoň prvního má právě n komplexních kořenů, počítáme-li je včetně násobnosti.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.