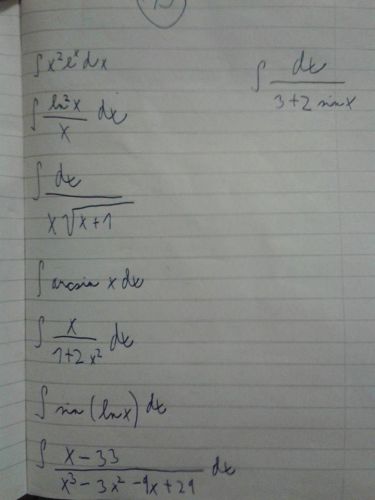Zdravim nemozem vypočitat 2 integraly , ten uplne dole a ten na pravo hore keby to niekto vedel tak budem vdacni.
0x
První z kritickích příkladů se obecně počítá rozkladem na parciální zlomky; jen nepřečtu konkrétní cifry, není tam ve jmenovatelu absolutní člen 27?
Ve druhém zafunguje substituce tg x/2 = y
to je 29 v tom menovateli na konci. vedel by si to vipocitat a poslat to tu? dik.
doplněno 20.11.15 18:43:
dole to je nasledovne 3x-3xˇ2-9x 29
Teď ten jmenovatel chýpu ještě mí%n. Něco vám tam vypadlo, při nejmenším. Problém je v tom, že k řešení je třeba najít nukové body jmenovatele, a k tomu by bylo třeba znát ho přesně.
Tak ted je to jasné, ale bohuzel trochu problematické. Principiálně zůstává ta cesta přes rozklad a kdyby na konci jmenovatele byla 27, šlo by to celkem bez problémů realizovat (proto jsem se na to ptal; ono to dost vypadalo na devěta dvacífku, ale jist jsem si nebyl – můte to dobře opsáno?) . V této podobě to sice teoreticky jde, ale od pohledu nevidím, jak na to. Takže se ještě podívám, není-li tam skrifá finta, aale nevím, nevím.
Zkuste aspoň tu substituci.
Ako je mozne aj to ze som to zle odpisal ale to uz nezistim lebo nemam to zadanie. Ale vipada to tak ze tam bude ta 27
To je docela pravděpodobné. Pak by se jmenovatel upravil takto:
x³ − 3x² − 9x + 27 = x² (x−3) −9(x−3) =9 (x−3)*(x²−9) = 9 (x−3)² (x+3) a z toho už není problém odvodit rozklad na parciální zlomky; zvládnete to?
Pokud by tam byla 39, jeden z kořenů by byl jako na přiložeém obrázky (viz folfram alfa) a s tím by se dost těžko pracovalo; pochybuji, že by to někdo takhle zadal.
doplněno 21.11.15 13:40: dopustil jsem se překlepů, speciálně jsem chtel napsat "kdyby tam bylo 29...", a taky v úpravě jmenovatele jsem omylem zapomenul devítku, závěr má být(x−3)² (x+3) Vrátím se k tomu dále.

Tak možná bychom se mohli bavit o těch jednoduččích, ale když uř jste se ptal na tenhle, pojďme na něj (třeba vám zpětně pomuže i u těch lehčích.´
Bydu tedy předpokládat tvar jmenovatele
x³ − 3x² − 9x + 27 ,
který upravím následovně (to uý jsem psal, ale dopustil jsem se přepisu; taky tu úpravu předvedu podrobněji):
x³ − 3x² − 9x + 27 =x² (x−3) −9(x−3) = (x−3)*(x²−9) = (x−3)*(x−3)* (x+3) = (x−3)² (x+3).
To umožní rozklad xlomku na parciální zlomky. To jste si jistě říkali, tak o tom nebudu mluvit obecně (to si najděte v přednáškách), jen uvedu, že v tomto konkrétním případě rozklad integrandu na parciální zlomky vypadá takto:
(x−33) /[x³ − 3x² − 9x + 27] = A/ (x−3) + B / (x−3)² +C /(x+3),
kde A,B,C jsou (zatím neeznámá ) reální řísla. Ta čísla určíme metodou neurčitých koeficientů; studovanou rovnost vynásobíme společným jmenovatelem, roznásobíme a porovnáme koeficienty u stejných mocnin (jde to i jinak, určitě jste si to říkali). Tak to nejdříve zkuste sám, já to teď odešlu, dřív než to omylem smažu a vrátím se později.
Tak pojďme dál.
Máme určit A, B a C ze vztahu
(x−33) /[x³ − 3x² − 9x + 27] = A/ (x−3) + B / (x−3)² +C /(x+3)
Vynásobíme společným jmenovatelem, tedy výrazem
[x³ − 3x² − 9x + 27] = (x−3)² (x+3):x−33 = A*(x−3)(x+3) + B*(x+3) + C*(x−3)² Konstanty A,B.C lze určit například tak, že pravou stranu roznásobíme a porovnáme koeficienty u stejných mocnin na obou stranách; dostaneme soustavu rovnic, kterou vyřešíme-Předvedu jinou cestu:nejprve dosadíme x =3 a dostaneme−30 = 6B, B = −5Nyní dosadíme x = −3 a dostaneme−36 = 36C, C = −1Dalčí volba, při kdteré by se totho hodně anulovalo, už není k disposici- Ale když dosadím za C, B právě vypočtené hodnoty, dostanu vztahx−33 = A*(x−3)(x+3) +−5(x+3) −(x−3)², do kterého mohu dosadit za x cokoli, nejlépe x =0:−33 = −9A −15 −9výpočet už nechám na vás. No a když pod integřítko napíšu tenhle rozklad, již to snadno zintegruji; nebo ne?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.