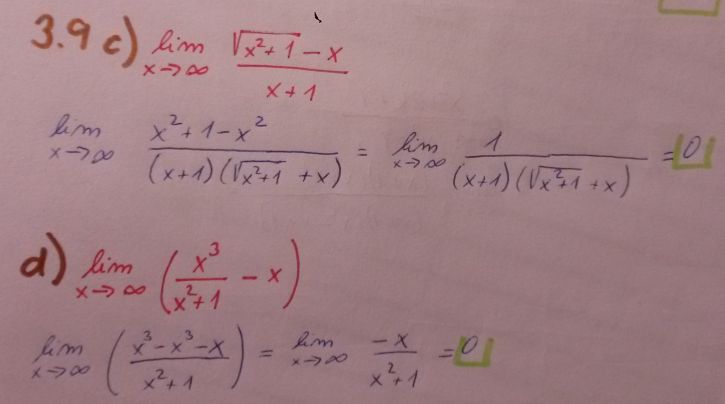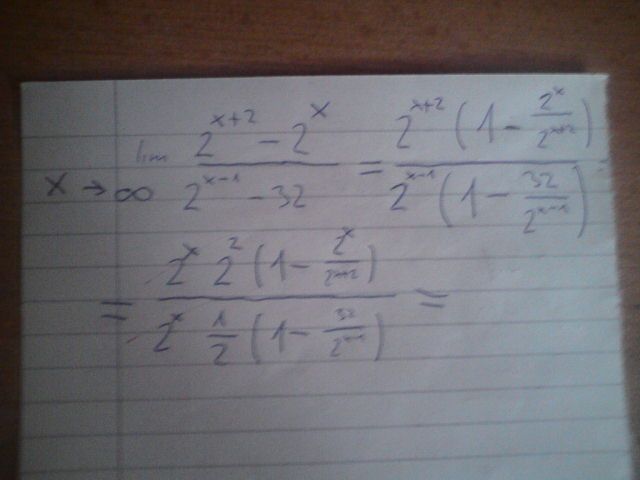Zdravím jak se počítají limity tohodle typu, třeba a)
A u toho řešeného příkladu d) nechápu té úpravě
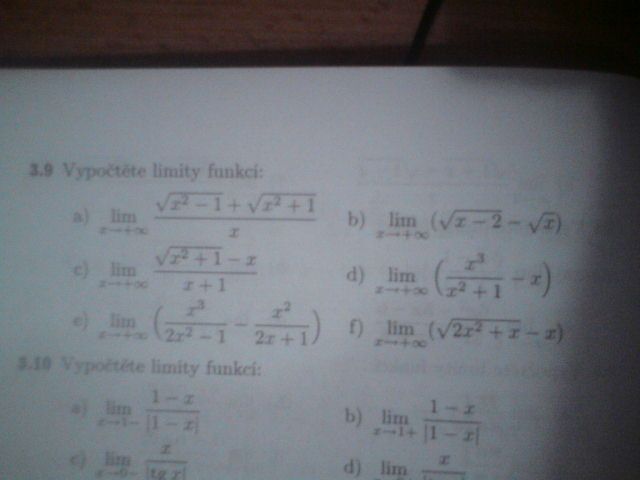
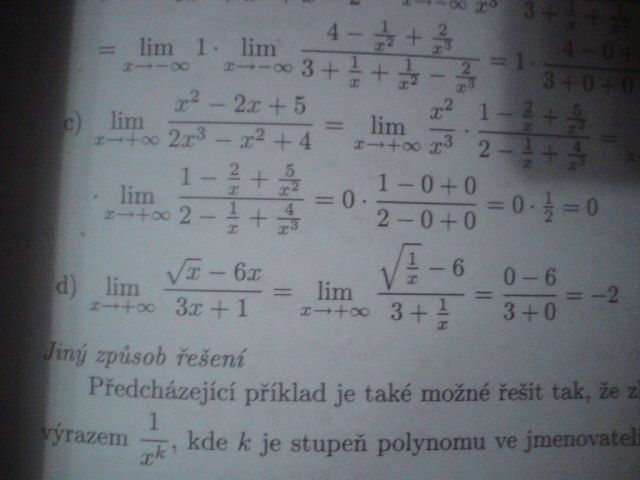
x jdoucí do nekonečna pod odmocninou vám taky půjde do nekonečna...i kdyby to byla třeba miliontá odmocnina.
Je to dobře, jenom trochu zbytečně složitý...v čitateli si zase ten zlomek vykrátíte- 2^x/2^x*2^2= 1/4, takže 3/4*4=3 a dole ve jmenovateli, ten zlomek půjde k nule, je to opět a/nekonečno, takže vám tam zbyde 1/2 a celý se to rovná 6.
Já bych ale začala tím, že bych si jmenovatel a čitatel vykrátila 2^x, takže vám tam rovnou vypadnou ty problémový mocniny a je to hned hotový...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.