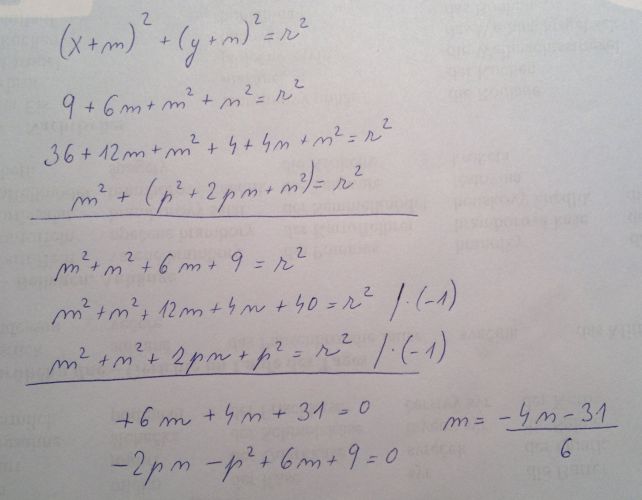Kružnice početní příklad

Od: lucka12345* 30.10.15 22:54 odpovědí: 5 změna: 31.10.15 13:50

Dobrý den, prosím o pomoc s řešením příkladu: Určete střed kružnice, která prochází body A[3;0]; B[6;2]; C[0;p]. Proveďte diskusi vzhledem k parametru p. Já jsem to dělala podle rovnice: x*x+y*y+ax+by+c=0,dosadila jsem souřadnice A, dostala jsem 1 rovnici, pak jsem dosadila B, mám 2.rovnici a dosadim C to je 3.rovnice a pak bych dělala soustavu rovnic, ale vůbec nevím, jak mám na to jít...a pak jak se má provést nějaká diskuse vzhledem k parametru p, tak to nevím, co tam mám dělat... Děkuju

Odpovědět na otázku Skočit na nejnovější odpověď

5 odpovědí na otázku

Řazeno dle hodnocení

elisa24®

30.10.15 23:04

To máš dobře, vyřešíš tu soustavu rovnic a parametr p určíš podle toho, že poloměr kružnice musí být kladný.

lucka12345*

30.10.15 23:27

Mě nejde vyřešit ta soustava..já bych potřebovala aspoň vědět první krok,co mám udělat..

elisa24®

30.10.15 23:42

Jestli je tam nějaká numerická chyba, tak se omlouvám, ale postup by měl být správně.

kartaginec®

31.10.15 13:34

To určení parametru p je špatně. Viz níže.

doplněno 31.10.15 13:51:

Myslím tím tu diskuzi.

Skočit na otázku
Vložit novou otázku

[přidat komentář]

kartaginec®

31.10.15 13:50

K té diskusi vzhledem k p, podívejme se, jaký má smysl. Nejprve geometrický význam: Tři body určují kružnici. A to jednoznačně a vždy tehdy, neleží-li ty tři body v jedné přímce. (Vlastně i tam určují alespoň "zobecněnou kružnici"o nekonečném poloměru. tak někdy chápeme přímku.) Takže diskusi byste vlastně mohla provést dřív, než začnete úlohu vúbec řešit: stačí zjistit, pro jaká p je vektor C −A násobkem vektoru B −A; taková p budou "zakázaná"a úloha bude řešitelná pro všechna ostatní p. To ale využíváme znalostí geometrických, pokud tedy k úloze přistupujeme čistě početně, musíte sestavit ty tři rovnice a pak zjišťovat, při jakém p budou/nebudou řešitelné (samozřejmě výsledek musí být tentýž).Při postupu vámi navrženém byste dostala tři rovnice3a + c = −96a + 2b + c = −40pb +c = −p²(v těchto rovnicích není poloměr r obsažen explicitně a také souřadnice středu jsou skryty v těch koeficientech a, b, c; vše musíte dopočítat doplněním rovnice x*x+y*y+ax+by+c=0 na čtverec. (Vyjde m = a/2, n = b/2, r² = ¼ (a² + b²) −c, ale ten poslední výraz nás vlastně nezajímá, na ten se nikdo neptal. Samozřejmě by měl být kladný, ale protože této rovnici vyhovují hned tři body, A, B i C, a výraz (x + a/2)² + (y + b/2)² je kladný, je kladný i dotyčný výraz, který je mu roven. Tak a teď k řešení. Chcete-li pokračovat v řešení podle vlastní ideje, potřebujete řešit systém tří rovnic pro tři neznímé a, b, c. Nevím, co o takových systémech víte a jaké metody znáte na jejich řešení, co jste o tom brali. Ale pokud chcete první krok, mohla byste třeba od druhé a třetí rovnice odečíst tu první a řešit dvě rovnice pro dvě neznámé a, b (neznámou c byste vyloučila). Anebo můžete zkusit postup, který poradila @elisa24. Ten má na první pohled nevýhodu, že ty rovnice jsou kvadratické, ale jak se ukazuje, všechny kvadráty m, n a r se eliminují. Zato má výraznou výhodu v tom, že hledaná rovnice už explicitně obsahuje hledané souřadnice středu. Provda, není to dotaženo do konce, ale to jste ani nechtěla, ne? A diskuse? Pro určité p ty rovnice nepůjdou vyřešit. e-matematika.cz/...

Skočit na otázku
Vložit novou otázku

[přidat komentář]

Přidat svou odpověď

Přihlásit se k odběru odpovědí z této otázky:

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.

Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.