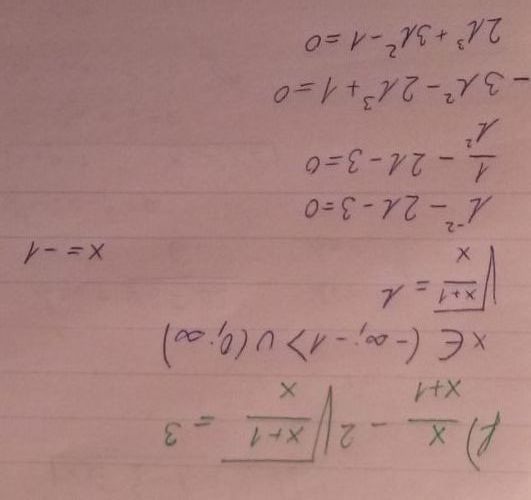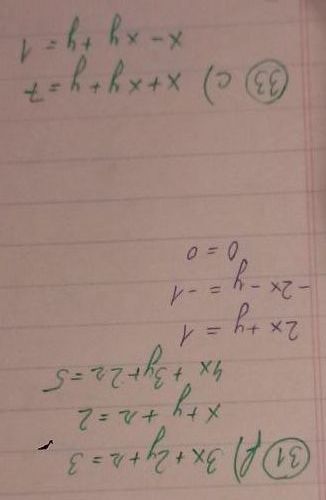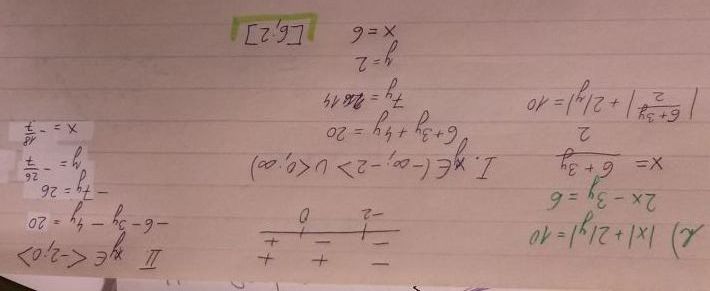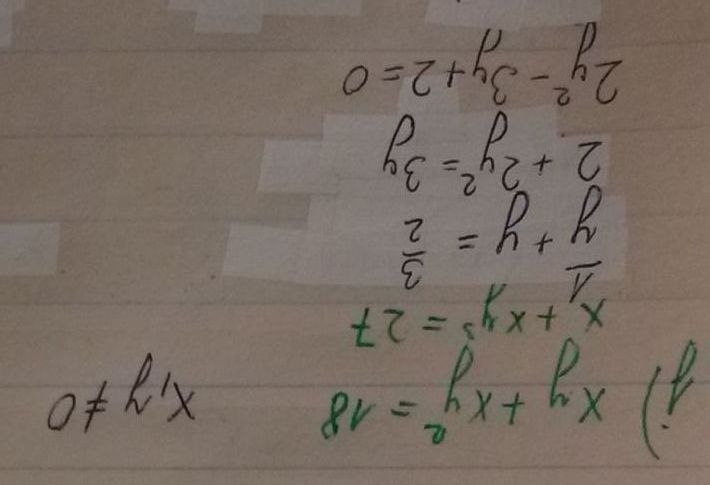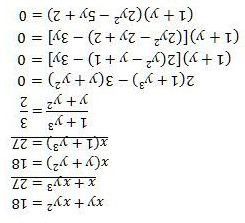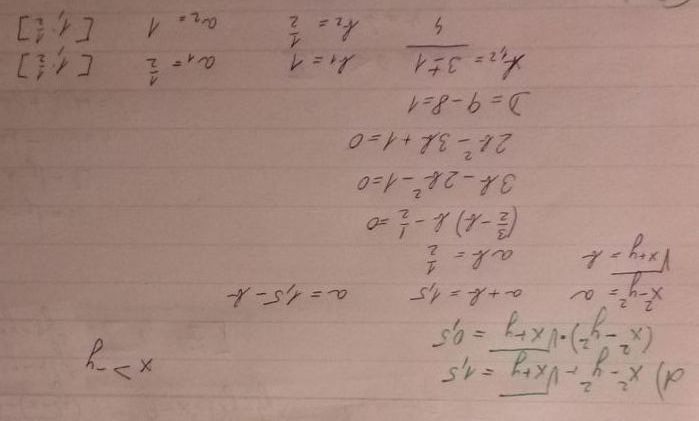Dobrý den, jak se prosím počítají tyto soustavy rovnic? Mockrát děkuji
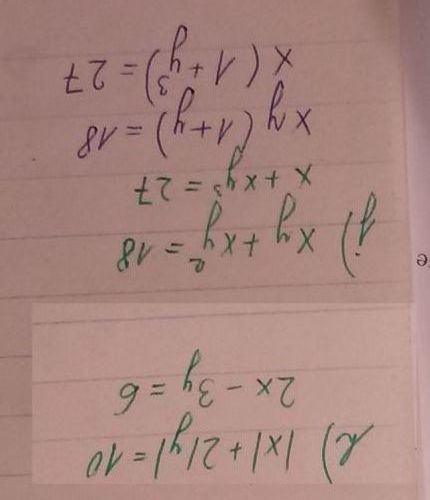
2x
Už jsem z toho trochu vypadl, ale tak ten bod h) je jednoduchý, ale relativně pracný, tak jsem si ho zkusil vyřešit. Ale stačí si vyjádřit x z druhé rovnice, dosadit do první a tu první pak pochopitelně řešit jako normální jednu rovnici s absolutními hodnotami, takže určit si nulové body atd. Samozřejmě je potřeba dávat pozor na to, která řešení jsou opravdu řešeními, a na konci to ověřit zkouškami. Byla to zábava, i když ne ve všech případech úplně hezká čísla. Hodně zdaru.
doplněno 28.10.15 21:35:
To poslední je taky zívačka. Ty dvě rovnice jsou si natolik podobné, že by člověka mělo hned napadnout, jak je upravit, aby se zbavil toho či onoho. Pak už vyjádřením neznámé z jedné rovnice se z té druhé stane kvadratická a hurá, řešení je na cestě.
Děkuji, h) mi vyšlo [6;2].
Jsou nějaké podmínky pro x? V tomto případě bylo pro y (-nekonečno;-2> a <0;nekonečno), určí se podle toho i podmínky pro x?
U posledního příkladu mě napadá jen je sečíst, ale 2x+2y=8 to mi nepomůže.
doplněno 28.10.15 21:58:
Aha, a pak do této rovnice dosadit za x nebo y. Děkuji
To jen jedno z řešení, 6 a 2. Je jich víc. ![]()
Když y vyjde z příslušného intervalu, tak jsem to bral, že i z té druhé rovnice dopočítané x je řešením, protože ta druhá rovnice je normálně lineární. A zkoušky mi to ve finále potvrdily. Jinak pro to y je ten první interval otevřený a chybí ti ten interval mezi, který je taky důležitý, že ano.
Jedna možnost je sečíst, ale samozřejmě 2x + 2y = 8 je totéž jako x + y = 4. A druhá možnost, jaké to překvapení, je je odečíst.
Není to násobení, nedají se ty dva intervaly sloučit. Jsou tři intervaly, (-nekonečno ; -2), kde se u obou absolutních hodnot změní znaménko, <-2 ; 0), kde se změní znaménko jen u té druhé, a nakonec <0 ; +nekonečno), kde zůstanou obě jak jsou.
K rtěm podmínkám na x: u příklladu h když počítáte tak, jak počítáte (tedy výpočtem x z druhé rovnice a dosazením do rovnice první). tam žádné další podmínky na x nepotřebujete, ty už jsou schované v té podmínce y <>=<−2. Existuje ještě jeden postum, místo tří rovnic po dosazení řešit čtyři systémy před dosazením, x>0,y>0; x<0,y>0; x>0,y<0; x<0,y<0.
(jen aby bylo jasno tyhle "podmínky" nejsou podmínky toho duhu jako podmínka, že se nesmí dělit nulou; spíše bych mluvil o podpřípadech, které se řeší různě. Kdyby například při rozboru prvního případu, tedy y ≥ 0, vyšlo y = − 2, neznamenalo by to, že tkové y nemůže být řešením, pouze by nespadalo pod právě probíranou podmínku a tedy by tento postup o něm nic nevypovídal.)
Co se týče vlastního řešení, v tom vám dostatečně poradil @naihonn. Snad bych jen doplnil, že ty intervaly nemusí bít disjuktní, konkrétně mám na mysli, že v té rovnici h po dosazení za x interval od mínus nekonečna do mínus dvou může být otevřený, ale klidně ho můžeme vzít i uzavřený, i když pak bod y = −2 bude ve dvou intervalech. To souvisí s tím, že plus nula je totéž jako mínus nula; hlavne bod mínus dva nevynechat.
A k příkladu j: zkusil bych ty rovnice podělit (pozor na podmínku)
Proměnné a, b jste vypočítala. Teď stačí si uvědomit, že b² = x + y a tím pádem a/b² = x −y a máte soustavu dvou lineárních rovnic pro dvě neznáme. Tak řešte a nezaomeňte na podmínky.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.