Nejste přihlášen/a.
Mám úlohu a potřebuji poradit s odpovědí e
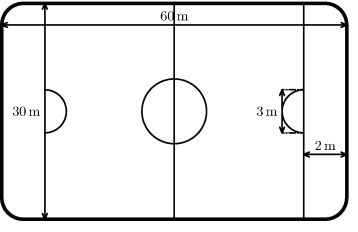
Jeden horký letní večer myslel Jindra na zimní prázdniny a na jeho oblíbený hokej. Když byl naposledy na stadionu, led byl perfektně kluzký, jen měl jednu vadu – kluziště nebylo vodorovné.
Jindra to poznal tak, že puk, který položil do středu kluziště, se začal sám bez tření klouzat přímo k jednomu z delších mantinelů. Stopkami Jindra změřil, že tato "cesta" puku trvá přesně 13,3 s. Toto zjištění ale Jindru moc nepotěšilo, neboť všechny rovné střely na bránu budou na nakloněném kluzišti vybočovat.
Jindra stojí ve středu kluziště a střílí přímo na střed branky rychlostí v1=4 m⋅s−1. Jak se domníval, bránu kvůli náklonu kluziště netrefil. Nakreslete, jak asi vypadala trajektorie puku, který Jindra vystřelil.
Vypočítejte, o kolik byla Jindrova střela odchýlena od středu branky v čase, kdy byla na úrovni brankové čáry.
Jakou nejmenší rychlostí v2 musí Jindra vystřelit, aby bránu trefil?
Jak velkou rychlost by měl takto vystřelený puk v čase průchodu brankovou čárou?
Určete velikost úhlu náklonu kluziště.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.