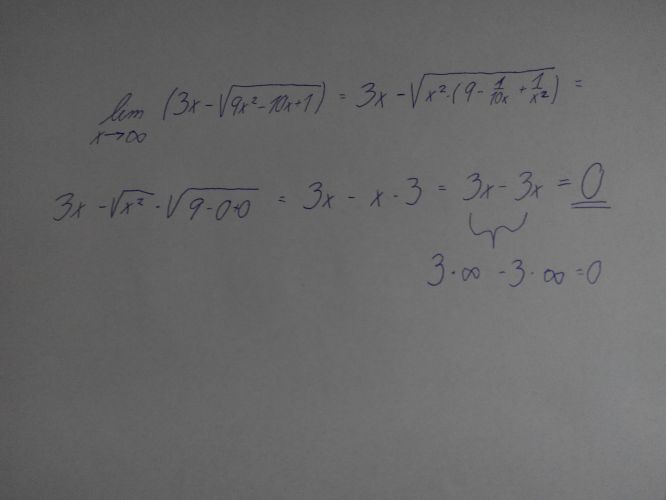Poradil by mi někdo zda tento příklad řeším špatně? mne vychází 0 dle výsledků to je 5/3..
Obecně nevlastní limity řeším tak, že vždy vytýkam číslo s největším exponentem, dostávám typové limity dle kterých počítám.. Nejspíše dělám chybu v tom že to nepřevádím jen na součet a rozdíly neznámých ale mám tam i násobení...Potřeboval bych asi nějáký obecný postup jak limity řešit.. ať už vlastní či nevlastní..
Díky moc za rady!
5x
Chyba, které jste se dopustil, má dokonce své jméno; říká se jí "částečné zlimitění". První úprava ( vytčení x zpod odmocniny) je celkem vpořádku, i když nám moc nepomůže. Ale následně jste zlimitil ten výra pod odmocninou, ale x před odmocninou jste si nechal na později. To nemůžete, k tomu nemáte oporu v žádné větě o limitách.
Možná ještě markantněji je to vidět, kdybyste ještě vytkl x z obou členů součtu. Představte si, že provedete tu svou první (správnou) ůpravu, pak ještě v tom druhém členu odmocníte x, ale to ostatní, co máte v odmocnině (tedy 9 – 1/10x + 1/x²) necháte pod odmocninou beze změny, já pro stručnist tu odmocninu i s tím, co odmocňujete, označím A. Procujete tedy s výrazem
3x –x*A.
To budu upravovat: 3x –x*A = x*(3–A). Limita A je 3¨,. ale nesmíte psát lim x*(3–A)=x*limA = lim (x*0) = 0. to je právě to částečné zlimitovámí. Věta, o kterou byste se měl opřít, je věta o limitě součinu, která má dvě nedílné součásti, totiž vzorec a předpoklady, za nichž platí; v našem případě zní
lim [x*A ] = (lim x)*(lim A). (toje ten vzorec), pokud (a ted přijdou podmínky) lim x i lim A existují a jejich součin má smysl. Čili znovu, nemůžete si nejdřív udělat jednu limitu a tu druhou si nechat napotom. A když náš příklad rozebereme, zjistíme, že obě potřebné limity sice existují, ale jedna je nulová, druhá nekonečná a nula krát nekonečno nemá smysl (někdy mluvíme o neurčitém výrazu, ale to je taky trochu nepřesné, zkratkovité vyjádření, tak to teď nebudu rozebírat). Tedy podmínky nejsou splněny a věta je nepoužitelná (tedy ne, že neplatí, ale nemúžeme z ní nic vyčíst).
Tolik k chybě, kterou jste udělal. Správnému postupu věnuji další odpověď (pokud se mezitím neozve někdo jiný).
3x
Takže teď bych se vrátil ke správnému řešení. Ano, měl byste znát nějaké obecné postupy; schválně používám množné číslo, protože jeden univerzální postup neznám. Na něco podobného jste se už ptal a nedovedl jsem vám poradit. Tohle je ale konkrétní příklad a o tom se pobavit můžeme.
To je výraz typu lim [√ A(x) − √ B(x)] . Pokud existují limity lim A(x) = A, lim B(x)=B a výraz √A − √ B má smysl, pak existuje i hledaná limita a rovná se tomuto výrazu, Problém nastane, když A i B jsou nekonečna, protože nekonečno mínus nekonečno smysl nemá (někdo řekne, že je to neurčitý výraz typu nekonečno mínus nekonečno). Pak zkoušíme tento postup: [√ A(x) − √ B(x)] vynásobáme a vydělíme (tedy rozšíříme) výrazem [√ A(x)+√ B(x)]. Dostaneme výraz [A(x) − B(x)] / [√ A(x) − √ B(x)] , kde v čitateli odmocnimy zmizely a to může pomoci. Zatím si to zkuste, já konkrétní řešení napíšu zase do další odpovědi, abych text nepřetěžoval.
1x
Uprav tak, aby pod odmocninou byl výraz (1 - ...). Pak rozepiš jen do prvního členu dle vztahu odm(1-x) = 1- x/2 (to platí pro x blízké nule, což tady platí. A vyjde 5/3
to platí pro x blízké nule, což tady platí.
"x" neni vubec blizke nule. Prave naopak - je zadano, ze "x" je nekonecno. ![]()
rozepiš jen do prvního členu dle vztahu odm(1-x) = 1- x/2
On ma vysledek spocitat, ne priblizne odhadnout, coz tento oriznuty rozvoj odmocniny do polynomu dela.
Pardon, tedy podrobněji, ať někoho nematu.
Uprav tak, aby pod odmocninou byl výraz (1 - ...). Pak rozepiš jen do prvního členu dle vztahu odm(1-y) = 1- y/2 (to platí pro y blízké nule, což tady platí. A vyjde 5/3.
Sakra, to byla chyba na moji strane s tim "x". V te rychlosti jsem si neuvedomil, ze toto "x" neni to same jako "x" ze zadani.![]()
To nicmene neresi ten problem s nahradou jedne funkce za jeji polynomialni aproximaci, navic jeste zkracenou (tj. zamerne pribliznou).
V tomto konkretnim pripade to nema vliv na vysledek, ale to je jen nahoda.
doplněno 20.10.15 10:00:
Na duhou stranu je pravda, že pokud tyhle všechny tyhle věci umím, je vaše cesta nejrychlejší, a i když to někdou neumí, lze mu na tomto postupu zkusit objasnit (ne vypočítat), proč ta limita vyjde právě tolik a jak ten mechanismus vlastně vnitřně funguje.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.