Ahoj, potřeboval bych poradit, co provedli na přiloženém obrázku v prvním a třetím řádku za závěrečnou úpravu výrazu? Předpokládám, že se jedná o tu samou fintu. Příklady na obrázku jsou závěrečné úpravy tří příkladů - v tom prostředním vytknuli (x-y), ale řeba v tom posledním vůbec nechápu, jak se ta dvojka dostala před (7b-5). Poradíte?
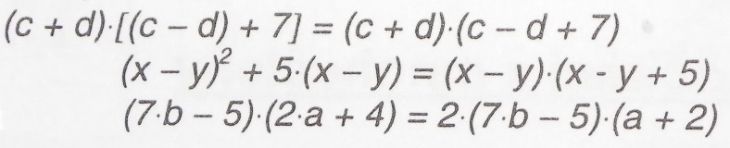
3x
S "názvy" bych se zas tak netrápil, i když je dobré umět svůj postup popsat. Takže: v tom prvním příkladu jste odstranil nadbytečnou závorku. Ve druhém případě jste vytkl (x–y) a vlastně jste taky mlčky odstranil nadbytečnou závorku – tu úpravu lze rozepsat jako (x–y)² + 5(x–y) = (x–y)[(x–y) + 5 ] = (x–y)(x–y + 5). a na posledním řádku jsme vytkli z druhého dvojčlenu dvojku, a na začádek se dostala výměnou (přehozením) s první závorkou díky komutativnímu zákonu, což je úprava natolik triviální, že málokdo by vůbec cítil potřebu ji komentovat (ale jak vidno, někdy je to vhodé).
No to trochu záleří i na tom, k čemu to potřebuji. Tak například z té úpravy poznám, že pokud jsou a, b přirozená čísla, je ten výraz sudý, a pokud mi to k něčemu je, tak je mi k něčemu i ta úprava. Nebo pokud jde o součást větších úprav, v jejichž průběhu se mi může hodit další vytknutí (a + b). tak taky. Jinak moc velký rozdíl mezi tou levou a pravou straou není, ale přeci jen ta pravá strana vypadá poněkud jednodušeji, nebo chcete-li, elegantněji.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.