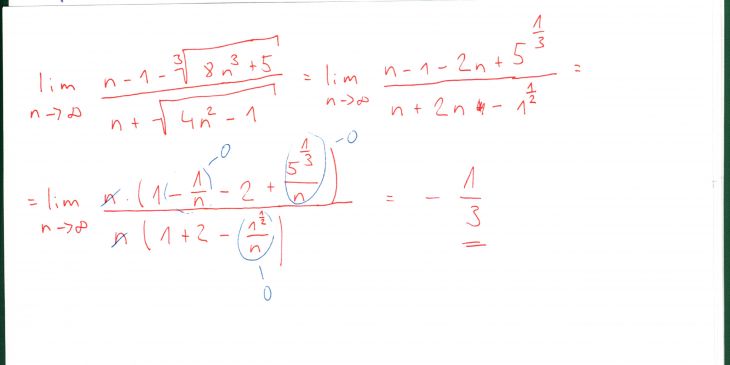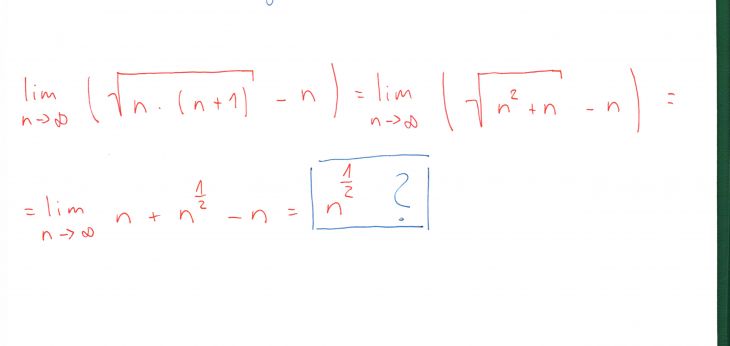Nejste přihlášen/a.
Zdravím, mám dvě otázky na limity. První příklad je pouze pro kontrolu, ten bych měl mít správně. Jen si tam nejsem jistý tím správným vytknutím konkrétně u toho 51/3/n, ale mělo by to být OK.
Ten druhý příklad je ukázka toho jak jsem to počítal.. no nicméně by to mělo vyjít pouze 1/2. Pokud by mi někdo mohl přiblížit jak se k tomu dopracovat, byl bych vděčný.
ps: omlouvám se za svůj škrabopis.. :D
1x
Máš to určitě blbě - odmocnina součtu (nebo rozdílu) není součet (rozdíl) odmocnin, stejně jako například
(a + b)3 není a3 + b3
doplněno 25.08.15 07:08:Shodou okolnosti ten 1.priklad pocitany spravnym postupem vyjde take -(1/3).
doplněno 25.08.15 07:46:Druhy priklad je pro me logicky naprosto nepochopitelny! Selskym rozumem mi jasne vyplyva, ze se to bude blizit nule, nicmene vypoctem opravdu vyjde (1/2) ![]()
![]()
Reseni:
predstav si te vyraz jako zlomek (tedy cely nad jednickou).
Rozšiř zlomek sdruzenym (?) vyrazem: √[n.(n+1)] + n (vsimni si toho plusu).
uprav horni cast zlomku podle vzorce (a+b).(a-b) = a2 - b2
dole ve zlomku vytkni "n" pred odmocninu
dole vytkni "n" z celeho vyrazu
pokrať "n" z horni a dolni casti zlomu (nahore ti zbyde jen "1")
0x
Obě tyto limity patří k takzvaným "neurčitým výrazům" (tohle pojmenování je malinko nepřesné, ale používané a tak do toho nebudu rýpat).
K prvnímu výrazu: Čitatel je vlasně "nekonečno méně nekonečno", ale poměrně jednoduché. Nejprve naznačím, v čem ta jednoduchost spočívá, tyhle úvahy budou trochu nepřesné a spíše heuristické (Heuréka! – Nalezl jsem!), ale mohly by přispět k pochopení. První nekonečno v čitateli je dáno členem n (vlastně n–1, ale tu jendičku můžeme zanedbat), od něj odečítáme nekonečno v podobě třetí odmocniny z 8n³ + 5, což se bude v nekonečnu chovat jako 8n³ (zase pětka je zanedbatelná), čili vlastně odčítáme třetí odmocninu z 8n³ (plus něco, co nehraje roli), (Tím se vysvětluje, proč tazatel dostal špatným postupem správný výsledek. On to "něco, co nehraje roli" napsal v podobě třetí odmocniny z pěti, což je sice špatně, ale když to nehhraje roli, tak na tom v konečném výsledku nezáleží. ) Takže čitatel se chová jako –n, celý zlomek je tím pádem "nekonečno lomeno nekonečnem", jmenovatel se bude chovat jako 3n a zlomek se bude (v nekonečnu) chovat jako – 1/3
Tak to bylo názorné vysvětlení, a teď výpočet. Ten nechám na tazateli, dám jen návod: Jak z čitatele, tak ze jmenovatele vytknu to rozhodující n. Ono bude v čitateli i ve jmenovateli ve stejné (první) mocnine, takže se pokrátí a se zbytkem bychom si měli poradit.
Já jsem se s tím nezabýval. Jen jsem letmo přečetl návod druhé limity od čtenář a už jsem se lekl, že nějak jednoduše vyloudil vytknutím n z odmocniny.
Totiž příklady ne jednoduchými, jistě již na úrovni minimálně střední školy, kde autor předvede takové znalosti jako viz odmocnění vícečlenu pod společnou odmocninou, se fakt nezabývám.
A navíc jsem v tom škrabopisu viděl osmičku a nikoliv nekonečno.
už jsem se lekl, že nějak jednoduše vyloudil vytknutím n z odmocniny
Jestli to je jednoduche nebo ne, to nevim, ale i ty jsi to spocital.
Jen pro uplnost napisu cely podrobny postup:
√[n(n-1)] = √(n2-n) = √{n2[1-(1/n)]} = √(n2).√[1-(1/n)] = n√[1-(1/n)]
Jedině, že pod odmocninou zbude 1+1/n pokud to k něčemu povede
To 1-(1/n) je dulezite proto, ze vime, ze limn→∞(1/n)=0 . Tedy z nekonecna se dostavame ke konecnemu cislu.
Cela myslenka pak je:
lim[√(1-1/n)] = √[lim(1-1/n)] = √[lim(1) - lim(1/n)] = √[1-0] = 1
doplněno 26.08.15 07:56:Vsiml jsem si, ze se ptas na 1+1/n a ja to ukazuji na 1-1/n. Vypocet s plusem je pochopitelne uplne stejny.
Tu správně spočetl čtenář, tak já jen dodám ty heuristické úvahy, abych mu vrátil ztracenou víru v logiku.
Uvahy uz nebudou zapotrebi, neb se ukazalo, ze Ctenar je osel, ktery neumi pocitat z hlavy a pouzivat kalkulacku.
Misto "√[n(n+1)] - n" si spocital par hodnot chybne pro "√(n2+1) - n" a divil se, proc mu to logicky pada limitne k nule, kdyz to ma vyjit 1/2 ![]()
V tom chybnem vztahu je "1" opravdu zanedbatelna proti "n". V tom "spravnem" tvaru je ale pod odmocninou dalsi "n".
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.