Log. rovnice

Od: filipino28391 14.08.15 00:12 odpovědí: 6 změna: 15.08.15 06:18

dobrý den, tak mám zase problém s rovnicí :D .. včera mi tu někdo poradil, jak spočitat exponencialni rovnici bez logaritmu ( logarimi moc nemusim :D ) tak jsem tu zase .. tentokrát se dvěma a přímo Logaritmickýma rovnicema:

Log₃X⁴-Log₃X³=2 a Log₈(X+1)+Log(X-1)=Log₈8

u první nevym co s tou dvojkou na konci a u druhy mi nějak nesedí že prostřední Logaritmus je dekadickej a zbylí 2 maj základ 8 ...

nejradči bych byl kdyby mi někdo pomoch a vypsal celej postup, ale budu rád i za radu co s tím :D

Odpovědět na otázku Skočit na nejnovější odpověď

6 odpovědí na otázku

Řazeno dle hodnocení

ctenar*

14.08.15 08:20

4log₃x - 3log₃x = 2

log₃x = 2 (obe strany hodit do mocniny 3)

3^log₃x = 3²

x = 3²

x = 9

(pripadne uz primo ve 2. radku jde psat z definice logaritmu, že x=3²)

2.priklad: vyuzij vzorec log_ba = log_ca / log_cb

Tim lze "menit" zaklady logaritmu:

log₈(x+1) + log₈(x-1)/log₈10 = 1

Fuj, to je osklive. Nejak me nenapada,co s tim, krome pochopitelneho (x+1)^log₈10(x-1) - 10 = 0

Asi v tom zadani bude preklep a vsechno to ma byt log₈.

doplněno 14.08.15 09:52:

Neco mi tam v te "osklive" rovnici vypadlo

(x+1)^log₈10(x-1) - log₈10 = 0

doplněno 14.08.15 10:13:

log₈10 je zhruba 1,1 coz je skoro 1, takze rovnice ma pak tvar: (x+1)(x-1) - 1 = 0 a to ma reseni x_1,2=±√2. Skutecna reseni nebudou zrejme moc daleko.

kartaginec®

14.08.15 09:44

Druhý přiklad vychází na první pohled divně. Jdu na kafe a pak se na to podívám, zatím by mohl tazatel zkontrolovat, jestli se nepřepsal v zadáníé.

kartaginec®

14.08.15 11:31

Dobrý rozbor. Mimo jiné je z něj vidět, že pokud v zadání skutečně tazateli vypadl ten základ 8, tak ta "správná" rovnice je vlastně velmi jednoduchá a vy jste ji vyřešil. (Jen doplním, že to vaše ±√2 je řešení odvozené kvadratické rovnice a původní logaritmcké rovnici vyhovuje jen to kladné z nich.) Pak by totiž na místě log810 bylo log88 , cořž je přesně jedna. To mě utvrzuje v přesvědčení, že v zadání má být Log8(X+1)+Log8(X-1)=Log88.Ještě pohled z druhé strany. o rovnici Log8(X+1)+Log(X-1)=Log88 = 1 mohu ihned říci, že její levá strana je spojitá a rostoucí, a to od mínus nekonečna do plus nekonečna, (a její definiční obor je x> 1). V důsledku toho je teoreticky jasné, že má právě jedno řešení, a toto řešení by bylo možné hledat nějakými numerickými metodami, třeba Newtonowou metodou, a u té bychom mohli jako první aproximaci a startovní iteraci vzít právě to x0=√2. Takře řešení existuje, ale silně pochybuji, že to je postup, který je po tazateli požadován, a nějaké řešení "v radikálech" či jinak rozumné si nedoedu představit. Sice se říká"nikdy neříkej nikdy", ale tady bych se toho odvážil.
doplněno 14.08.15 20:43:

Omlouvám se, zrušilo mi to indexy, Ale snad je to srozumitelné

filipino28391

14.08.15 20:09

dekuji moc za pomoc, příklady mám z učebnice pro 2. ročník střední školy takže se bude asi jednat o chybu v zadání (přepsané jsou dobře) mněli by to být základy logaritmú takťe nějaká Newtonowa metoda asi nepřicháztí v úvahu :D

ctenar*

15.08.15 05:56

Dobrý rozbor. Mimo jiné je z něj vidět, že ...
Vas rozbor je mnohem zajimavejsi. Velmi hezke cteni. Ja to takhle daleko pri rychlem psani sveho prispevku ani nedomýšlel.

ctenar*

15.08.15 06:18

Skutecna reseni nebudou zrejme moc daleko.
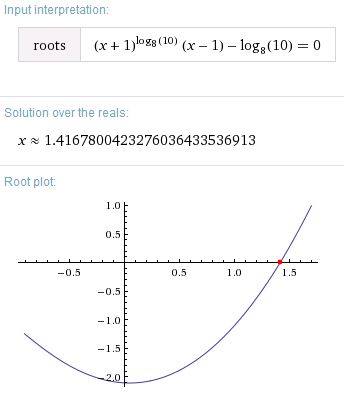
Co na to rika Wolfram?

x=1,41678004... (√2 = 1,41421356...)

Skočit na otázku
Vložit novou otázku

[přidat komentář]

Přidat svou odpověď

Přihlásit se k odběru odpovědí z této otázky:

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.

Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.