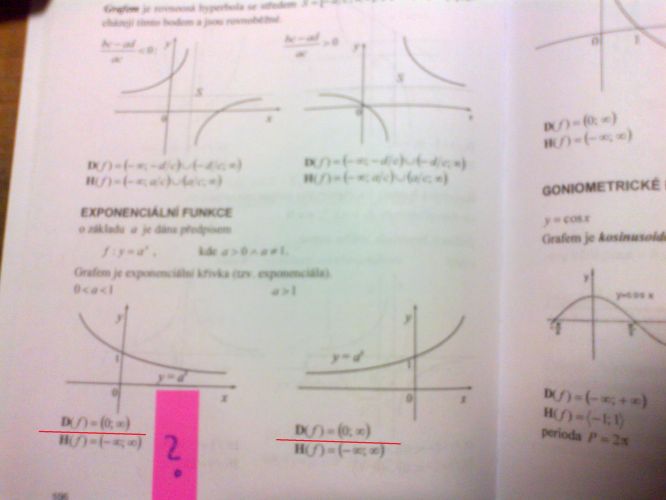
Ahoj, v učebnici jsem narazil na toto: Podle učebnice je definiční obor exponenciální fce (pro 0 < a < 1 i pro a >1) je D(f)=(0;∞
, neměly být to ale být včechny R neboli (-∞;+∞? Řekl bych, že to bude prohozené s oborem hodnot kde je H(f)= (-∞;+∞. Pravděpodobně to je banalita.. ale radši se na to ptám 
1x
V ucebnici je ten def. obor v poradku. Nikdy se nedostanes pod mensi hodnotu nez je 0, budes se k ni stale jen priblizovat.
Na prikladu to jde krasne videt. Pokud vezmes v uvahu, ze 0 <a <1, nezapomen zohlednit i obor hodnot, tak jakakoli hodnota z tohoto rozsahu dosazena za a se bude chovat nasledovne:
... az nekonecno
0.1-3 = 1000
0.1-2 = 100
0.1-1 = 10
0.10 = 1
0.11 = 0.1
0.12 = 0.01
0.13 = 0.001
... vysledek se cim dal vic priblizuje 0, kterou ovsem nikdy nedosahne
Jo aha, proč tam ale nemohou být záporná čísla - vždyť ve druhém kvadrantu graf má hodnotu i záporných x.
Naopak obor hodnot se nikdy nedotkne nuly (takže by měl být omezen ne?) a místo toho tam je (-nekonečno;+nekonečno)
No vždyť to říkám, a vy taky --- učebnice zaměnila obor hodnot a definiční obor. A gargamel jim na to naletél, popisuje sice (v podstatědobře, sice dobře, ale přeci jen trochu nejasně, co se týče jeho upozornění na "obor hodnot", patrně má na mysli omezení na základ a, které ale není zas tak podstatné, pro a> 1 se exponenciála bude chovat podobně, ale v mínus nekonečnu, a hlavně je to další zmatek v terminologii) chování oboru hodnot exponenciílní funkce, ale ne definičního oboru.
A jen ještě varování, co se týče té omezenosti. Patrně tohle víte a pouze jste použil stručné, byť nepřesné vyjádření: Funkce ax není omezená, ale je omezená zdola, a to ne proto, že se nedotkne nuly (i když v jistém smyslu to lze tak říci), ale prot, že neklesne pod nulu (a navíc aní té nuly nenabude).
0x
V učebnici se jim "povedl" v podstatě překlep: prostě zaměnili definiční obor a obor hodnot. Správně je Df=R, Hf = {y; y>0 (prostě to, co oni značí jako Df}
@gargamel jim na to "skočil". To, co píše, je dobrý popis (proto jsem mu dal jeden bod), ale právě toho oboru hodnot.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.