Co je to za zlomek?

Nevím kde bych ho měl hledat. V čase 40:50 nic na tabuli nepíše.

sorry 49:50

Pise tam jen: c=Δl/Δt (delta el deleno delta te), tedy vzdalenost za cas (coz je definice rychlosti). Vsechno co pise, tak i rika. Nevim, co neni jasne.

Nevim, o jakem kraceni mluvis. Poslouchal jsem az do 56:10 a to uz mluvi o jinem problemu.

Problém je v jednotkách. Pokud v klasické Newtonovské fyzice (a eukleidovské geometrii) zkoumáte rychlost, pak v definičním zlomku Δl/Δt (v klasické fyzice není rychlost světla nic specifického, Newton neznal teorii relativity a tak v jeho úvaháh není nic zajímavého,na tom, že tento zlomek pro nás definuje právě rychlost světla), tak jednotkou délky bude třeba centimetr (nebo míle, nebo třeba i versta, ale pro určitost zůstaňme u toho cm), a jednotkou času dejme tomu vteřina s. Zlomek Δl/Δt není podíl rovnocenných veličin, liší se přinejmenším rozměrem, což označujeme označením jednotky v hranatých závorkách: Δl = Δl[cm], Δt = Δt[s]. Hodnota rychlosti je tedy ono zmíněné v =Δl/Δ (přesněji toto je průměrné sychlost, respektyve rychlost rovnoměrného přímočarého pohybu, ale to teď není podstatné. Ovšem tato rychlost není "absolutní, světová konstanta, má rozměr, který dostaneme tak, že napíšeme

v[?] = Δl[cm]/Δt[s]odkud? = cm/^s–1 (centimetr za sekundu) Kdybychom měřili vzdálenost ve verstách a čas, co já vím, v klepsidrách, vyšla by jiná jednotka a samozřejmě i jiná číselná hodnota.V teroii (obecné) relativity je ovšem vše jinak. Zde pracujeme v časoprostoru a meci časem a vzdáleností není principiálního rozdílu. O tom je předchozí výklad, nepouštěl jsem si to celé, tak nevím, v kterých místech, ale to není v tomto okamžiku důležité. Podstatné je, že přednášející zavádí pro vzdálenost (ve zjednodušeném dvourozměrném zobrazení jde o jednotky na ose x) a pro šas (jednotky na ose t) stejnou jednotku, označím si ji pro okamžik j.Pak je

c = Δl/Δt = Δl[j]/Δt[j] , jednotky se zkrátí a rychlost světla vychází bezrozměrná (Následně ji přednášející poloří rovnu jedné, proč si to může dovolit, to už je jiná otázka, tomu je velká část výkladu věnována), ale tohle je podstata: v definičním zlomku pro rychlost se vykrátí jednotky, v nichž vyjadřujeme čitatele a jmenovatele.

dík už to chápu, akorát ještě by mě zajímalo co to jsou za znaky v tom zlomku, nějaké řecké písmeno. 28:40

Ono je tam těch písmen víc, ale předpokládán, že řecká písmena (fí, omega, ) jste poznal a ýe vám jde o takový to, co možná připomíná delta, ale delta to není, prostě znak ∂. To je znak pro parciální derivaci a pokud je mi zdámo, žádný zvláštní název to nemá. Jak o tom praví Wikipedie, Parciální derivace funkce f vzhledem k proměnné x se značí f x, ∂x_f, nebo ∂ f / ∂ x. Symbol ∂ se ustálil ve značení PD a je stylizovaným (zaobleným) písmenem "d". Oproti tomu derivace podle jedné proměnné se značí pouze písmenem "d" bez stylistické úpravy. A když už to chci přečíst, tak mohu říci d fí podle dé té, kroucené dé, parciální dé...

Toto značení PD poprvé použil Adrien-Marie Legendre, ale obecně se začalo uznávat až po jeho oživení Carlem Gustavem Jacobem Jacobim.

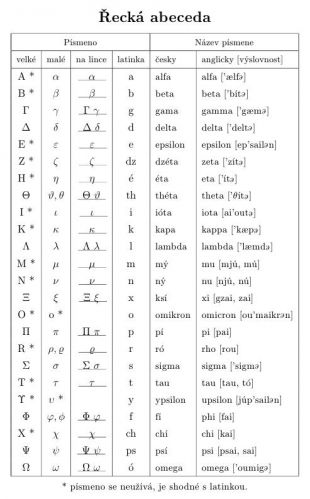
Řecká abeceda například viz obrázek

Obrázek zde

Zdravím, mohl bych ještě otázku k tomu samému videu, akorát v čase 33:13 jak dojdu k tomu a s čárkou = e^{i fí} krát a

Poté tam vysvětluje zakreslení kompl. čísel a vzorečky a ty pak doplňuje do tohoto.

Základ komplexních čísel mám, i logaritmický zápis a to jak pak dostaneme pak ty cosinusy a sinusy už vím.

Dík za pomoc, od vás to vždy pochopím

Pravděpodobně se ptáte na význam, respektive odvození vztahu

a’ = e^iζ * a

použil jsem dzéta místo fí, které zdejší editor nenabízí, tak mi to promiňte).(Pokud vám nebylo jasné něco jiného, tak napište.

Ono je to vlastně v tom videu podrobně vysvětleno, zkusím to jinými slovyVýznam je ten, že tahle zapíšete otočení komplezního čísla a o úhel ζ, čímž vznikne číslo a s čárkou.

Že číslo e^iζ je komplexní jednotka a je rovno cos ζ + i*sin ζ, to zřejmě víte, podle toho, co výše píšete, a víte také, že obecné komplexní číslo a lze zapsat buď v aritmetickém tvaru jako a = x +i*y, nebo v goniometrickém tvaru jako |a|(cos α + i*sin &alpha, víte také, ostatně to pak dále dr. Koláček také popisuje s kreslí. V tom druhém zápisu A =|a| je absolutní hodnota čísla a, které se také říká amplituda (tento název zde použi prof. Koláček), a úhel, zde označený α (pan profesor zase používá označení fí, ale to je jen označení) se nazývá fáze komplexního čísla, nebo též argument (což je v matematice obvyklejší, výraz fáze odpovídá tomu, že nám tady jde o fyziku a tam se to tak říká), ale geometrický význam je ten, že jde o úhel, který průvodič obrazu komplexního čísla a, svírá s reálnou osou.

Teď to odkliknu, než se mi to ztratí, a budu pokračovat v doplnění. Zatím se podívejte především, jestli skutečně odpovídám na váš dotaz. a také, jestli je to zatím jasné.

Pokračuji. Teď co je to zač, to násobení? Jak se násobí komplexní čísla? Jsou-li v aritmetickém tvaru, tak se to násobí tak, jak se roznásobují závorky.jen přitom využíváme toho, že i*i = – 1 (to umíte). Při násobení čísel v goniometrickém tvaru můžeme postupovat stejně (konec konců on je to vlastné taky aritmetický tvar: |a|*cos α je reílná složka a |a|*sin α imaginární). Ale, a co je důležité, pro goniometrický tvar platí:

komplexní čísla se násobí tak, že se násobí amplitudy a sčítají argumenty

speciálně to znamená, že násobení komplexní jednotkou (která má amplitudu jedna) je otočení o ůhel, rovný argunebtu (fázi) té jednotky; což tam pan profasor hned na začátku nakreslil a na závěr napsal.

Teď je ovšem otázka, proč se takhle násobí komplexní čísla. Rychlá, ale nikoli vyčerpávající odpověď je, že to říká Moivreova věta; ten tučný text je právě ona (respektive jedna z jejích možných formulací či variant). Pokud vám to stačí (čistš uživatelsky by i mohlo), tak to prostě vemte na vědomí. Ale tuto větu samozřejmě lze i dokázat, a to různš. Vhodný způsob záleží na tom, jak celou teorii komplexních čísel budujene, čím začínáme a co z čeho odvozujeme, ale možná byste to mohl zkusit i sám tak, že byste dvě komplexní čísla v goniometrickém tvaru roznásobil jako aritmetický tvar. Tím byste dostal ve výsledku nějaké ty součiny různých sínů a cosínů, a kdybyste na ně aplikoval součtové vzorce z goniometrie, vyšla by vám právě ta moivreove poučka.

Ano, odpověděl jste mi dobře na ten první vztah a děkuji . Komplexní čísla jinak umím s tím už jsem pak problém neměl. Akorát jak pak zapisuje tu transformaci do matice, tak na třetím řádku u zetka je 0 0 1. Vím, že ta zetová osa se nemění.

ahá parciální derivace, tak to mě nenapadlo, já pořád že nějaké řecké písmeno :D

dík moc, už to chápu