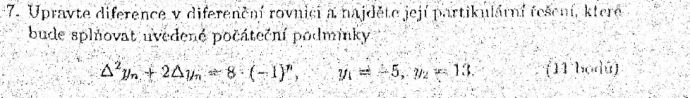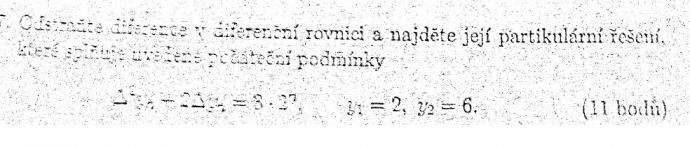Dobrý den.
Rád bych se zeptal, zda-li nevíte, jak spočítat tyto příklady? U obsahů nevím, jak nákresy rozdělit na části, podle kterých bych počítal obsah. Matice mi vyšla následovně:
Tak jsem to počítal znova a vyšlo
x1+ x2-x3=550
-x2-x3=-800
-x3-x4 +x5=-350
-2x4 +x5=-200
Podle zadání bych měl dosadit parametr za x3, což mi ale podle výsledků nesedí. Takže mám asi zase chybu ve výpočtu nebo nechápu, podle čeho dosadit parametr. Vaše názory?
Všem moc děkuji 
0x
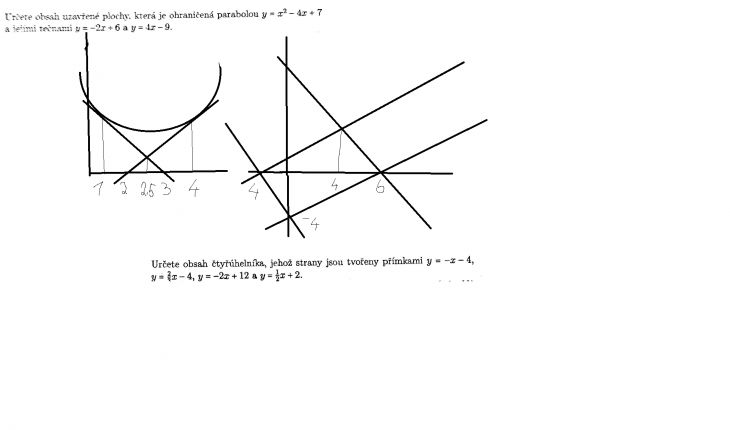
Zkusím Vám pomoc s druhým obsahem. Nevím, jestli náčrtky jsou originál, ale nulový bod rovnice y=-2x + 12 pro x mi vychází jinak než je náčrtek. Ostatní přímky jsou OK. Doporučuji zvolit měřítko 1 cm (nanést na osy x, y), pokud si pak trojúhelník nad osou x rozdělíte na 2 pravoúhlé, jak jste již naznačil, zjistíte délku odvěsen v cm a spočtete obsah obou pravoúhlých trojúhelníků. stejným způsobem pak vypočtete obsah trojúhelníku pod osou x.
0x
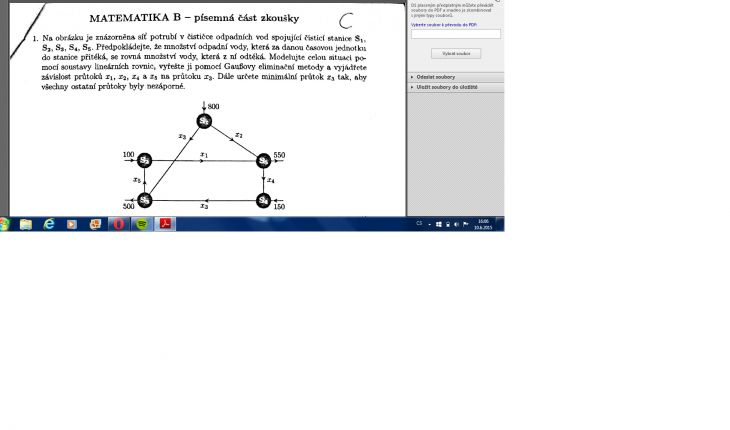
Je to nějaké zmateční. Jednak máte pět stanic a tedy byste měl mít pět rovnic. Dále namátkou ta vaše první rovnice neodpovídá nákresu. A podivnost je v samotném zadání, kde symbolem x3 jsou oznašeny dvě proměnné; pak by byl nsemysl chtít x3 zvolit za parametr, to ověem není vaše chyba, Nicméně takhle nedovedu poradit.
K dvojce se jen zeptám: nemáte ty obsahy počítat integrací? Ve druhém příkladu ji nepotřebujete nutně, ale v té jedničce by to bylo přirozené.
Neodpovídá zadání, protože to je už výsledek Ze zadání jsem sestavil matici upravil ji tak, aby byly nuly pod diagonálou. Pátý řádek se rovnal čtvrtému, pouze odlišná znaménka, přičetl jsem a pátý řádek tedy zmizel. H(A)=H(A)´, nekonečně mnoho řešení. Problém je, že nevím, jak ze zadání takových to příkladů poznat, za kterou x dosadit parametr. Jestli to je podle toho, že ostatní x jsou závislé na x3 a tedy bych měl dosadit "t" za x3. Ale podle výsledků nemám x3 ve všech řádcích matice, která mi vyšla. Takže buď to mám špatně spočítané, nebo něco jiného
Tak za prvé bych se zeptal, proč máte tuto otázku založenu dvakrát ? Nejen, že to pravidla zakazují, ale ono to taky trochu mate. No ale nevadí, pojďme se podívat na toto vlákno.
To, co jste napsal, opravdu neodpovídá zadání, i když vezmu v úvahu, že je to /částečné) řešení. V zadání máte k bodu 5 přiřazenu rovnici x1+ x2-x4=550 a pokud od této rovnice odečtete (S4) rovnici x3-x4=150, dostanete x1+ x2-x3=400, což je z vaší rovnicí ve při a systém by byl neřešitelný, což nejspíš není. Možná to je ta chyba?
Takže zkuste to projít ještě jednou. Zřejmě skutečně dostanete čtyři nezávislé rovnice pro pět neznámých. A co pak? Jestliže v zadání je "vyjádřete průtoky v závislosti na x3" , tak s tím začněte; položte x3 = t, výrazy s t převeďte na druhou stranu a řešte tytto 4 rovnice (tady jsem ve svém prvním příspěvku trochu ujel, sorry). Měl byste dostat x1,x2, x4 a x5 jako lineární funkce x3. Nezápornost těchto průtoký pak dává systém 4 nerovností, ke kterému byste měl přidat ještě nezápornost x3 a najín jejich nejmenší společné řešení.
Pokud vám to ani teď nevyjde, podívám se na to podrobněji.
doplněno 12.06.15 10:48:Ještě k té volbě parametrů: "Obecně"lze v takovém systému (n nezávislých rovnic pro n+1 neznámých volit jako parametr kteroukoli z nich, ovšem jsou případy, kdy se systém rozpadá ne dva či více podsystémů a tam lze volit jen některou z nich (volitelná proměnná). Jednodychý příklad je systém x + y ´a, z = b. (Je-li hodnost matice menší než počet proměnných o dva a více, je situace podobná, jen trochu slořitější.) Které proměnné jsou volitelné, zjistíte třeba při Gaussově metodě; rozhodně není na závadu fakt, že se ta podezřelá proměnná nevyskytuje ve všech rovnizích, ona se do vyjádření ostatních proměnných může dostat "zprostředkovaně"ve vyjádření těch ostatních, se kterými rovnici sdílí. Jednoduchý příklad:
x+y = 1
y + z = 2
zvolme za parametr z = t, dostaneme y = 2–t, x= 1 –y= –1+t.
V našem případě se po vás vysloveně chce, aby parametr byl x3. Pak si můžeme zjednodušit práci tím, že hned na začátku označime x3= t, převedeme na druhou stranu a Gaussovské úpravy provádíme s těmi zbylými "volnými "neznámými.
Povedlo se vám již příklad vyřešit? Já si ho stejně dopočítám do konce a kdybyste stále mělnejasnosti, tak se na to mrknem.
Protože jsem potom chtěl doplnit i ty obsahy. Doufal jsem, že to správce smaže
Děkuju! U všech těchto příkladů je, že máme určit minimální průtok např. x2, aby ostatní byly nezáporné. Když vypočtu matici, dosadím parametr t za x, na kterém ostatní závisí (např. x2). Tak jak potom zjistím ten miminální průtok? Nějakým výpočtem, grafem? Vím, že mám ostatní x dát rovno větší nule. Pokud vyjde například x1=t -100, tak t je větší rovno 100. Tak to udělám u všechn zbývajících x. A jak potom prosím zjistím ten miminální průtok např. x2, aby ostatní byly nezáporné?
Takže pokud tomu dobře rozumím. Minimální průtok x2 tak, aby ostatní byly nezáporné zjistím, když např. x1=100-t, x3=300+t, bude t menší rovno (násobení mínus jedničkou, abych měl kladné t) 100, t bude větší rovno -300. A obě "téčka" nahradím x2. Čili výsledek tohoto smyšleného případu bude?
Jak postupuju dál, narážím na další otázky :D Tentokrát ohledně diferenciálních rovnic. Překopíruju Vám můj dotaz na kolegyni, která ale nevěděla Učím se na zkoušku z matiky a řeším diferenciály druhého řádu. Naučil jsem se ta pravidla - když je jeden z kořenů 1, tak pravou stranu násobím n. A když je jeden z kořenů číslo, kterým na pravé straně násobím, zase pravou stranu vynásobím n. Propočítávám příklady a narazil jsem na dva případy. Jednou mi vyšly kořeny plus minus jedna a vpravo bylo násobení minus jednou na n. Čili jeden z kořenů se rovná číslu, kterým násobím a druhý z kořenů je ještě k tomu jednička. Takže prvou stranu vynásobím n nebo n na druhou? A potom druhý případ je, že mi vyšla v kořenu jednička, ale na pravé straně jsem násobil dvojkou. Čiliže zase propojení dvou pravidel. Příklady, kdy vyjde plus minus jedna aa násobím minus jedna na n+ příklad, kdy násobím dva na n a jeden z kořenů vyjde jedna.Pravá strana u prvního příkladu: yn=A*n*(-1) na n, yn+1=A*n+1*(-1) na n+1, yn+2=A*n+2*(-1) na n+2. Násobil jsem pravou stranu n, protože kořen vyšel minus jedna, což odpovídá pravidlu, že když vyjde kořen jako číslo, kterým násobím, mám násobit n. Ale kořen vyšel i plus minus jedna, čili i ta kladná jednička, u které se taky násobí n. Takže správně takto nebo jsem to měl vynásobit n na druhou, protože jsou obě podmínky splněny?Pravá strana u druhého příkladu stejná. Jenom násobím dvojkou na n. Kořen vyšel plus minus jedna.Mám to prosím správně nebo ne? 
já se na to mrknu, ale ne hned. Snad jen připomínka- ty rovnice nejsou diferenciální, ale diferenční
Ten první příklad mi vyšel ještě pěkně. Po všech dosazeních a úpravách mi zbylo 2A=8, čili A=4, což přičtu k "prvnímu výsledku" (C1 * kořen na n plus C2 * kořen na n).
U toho druhého příkladu mi vyjde 3A na n + 8A = 8. Což mi přijde divné. Pro 3A na n není nic na pravé straně. Teď jsem enkem pravou stranu nenásobil, takže po dosazení a vyškrtání dvojky na n mi zbylo 4a-a=8. Což už mi přijde logičtější. Tak se v tom plácám a nevím, co je správně a co ne
A teď jsem si všiml ještě tohoto:
Na pravé straně bude např. pouze 7. Kořen vyjde 1. Pravou stranu vynásobím n, čili yn=An, yn+1=An+1 (An+A), yn+2=An+2A). Vyjde nějaké A, např. 7A, 7A=7. Do výsledku ale nepřipíšu jenom +1, ale +1n. Budu postupovat stejně, pokud bude na druhé straně např. to, co ve dvou výše naskenovaných příkladech? Myslím to tak, že výsledek bude např. C1*8 na n + C2*9 na n + 1n. Nebo ta jednička bude bez n? Ono to totiž potom ovlivňuje výsledek C1 a C2, pokud mám zadané podmínky. Chápu to tak, že pokud pravou stranu násobím n, kvůli pravidlům vyplývajících z výsledků kořenů, budu výsledky A, případně B a C násobit n a takto je zapíšu do prvního výsledku s C1 a C2. Pletu se? Kdyby mi vyšlo A=7, B=5, připsal bych + 7n + 5. Ale pokud násobím pravou stranu, pak připíšu + 7n na druhou + 5n?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.