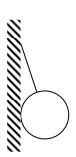
Voluntýř 028 Na tenkém vlákně délky l [m], upevněném na hladké svislé stěně, visí koule o hmotnosti m [kg] a průměru d [cm]. Určete tahovou sílu vlákna a tlakovou sílu, kterou koule působí na stěnu. Působící síly zakreslete do obrázku, gravitační zrychlení g = 10 m.s-2, velikosti sil uveďte v [N] na 1 desetinné místo.
Jaký je vzoreček?
2x
Vzoreček Vám nepomůže, je třeba pochopit. Řešení se skrývá v pravoúhlém trojúhelníku (takže ten vzoreček je Pythagorova věta). Strany trojúhleníka jsou d/2; l+d/2 a třetí, kterou je třeba dopočítat. Ve stejném poměru, jako strany trojúhelníka budou síly G (tíhová síla - odpovídá neznámé straně), (N tlaková síla - odpovídá d/2) a tahová síla (odpovídá l+d/2). To vše za předpokladu, že uvažujeme délku vlákna po povrch koule, nikoliv do jejího středu.
doplněno 08.06.15 13:14:Tíhová síla působí v těžišti - tím je střed koule a jde svisle dolů. Tlaková síla působí ve styčném bodě stěna - povrch koule a to kolmo na stěnu (tedy rovněž prochází středem koule) Tahová síla působí ve směru vlákna. Tíhovou sílu G rozložíte na 2 složky - vodorovnou (tedy tlakovou sílu) a šikmou tedy sílu ve vlákně. Dohromady to dává pravoúhlý trojúhelník s poměrem stran viz. výše (odpovídá to poměru sil)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.