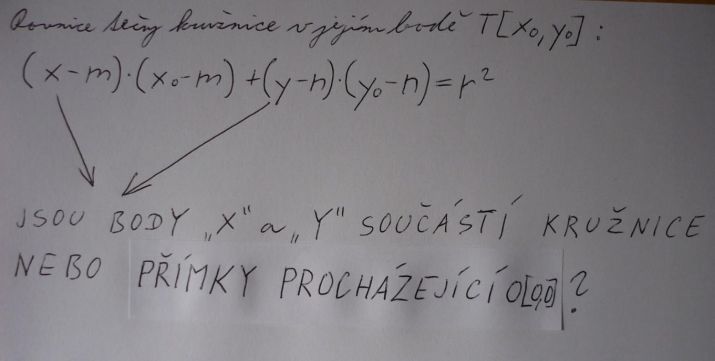Nejste přihlášen/a.
3x
Nevím, kde je chyba, kontroloval jsem začátek a ten je dobře; třeba tam ani chybu nemáte a jen jste to nezvládla dopočítat. Máte tam ale "strategickou" chybu: k dosazení do rovnice kružnice potřebujete vypočítat x + 5 a to v rovnici tečny máte přímo, takže roznásobením si to jen komplikujete. Já bych možná dosadil substituci x+5 = u, y + 5 = v a řešil systém
u²+ v² = 1
5u + 5v = 1
anebo bych dokonce rovnici kružnice vynásobil 25 a sybstituoval 1(x+5) = u, 5(y+5) = v;
zkuste to tak.
po úvaze jsem přesvědčen, že body "x" a "y" jsou součástí přímek a ne kružnice. Proto se tento vzorec nazývá rovnice TEČNY, čili rovnice přímky, která se dotýká kružnice v jednom místě.
Je to tak?
díky,
pro mě je hodně matoucí, že rovnice tečny přímky je hodně podobná rovnici kružnice. A v rovnici kružnice jsou body "x" a "y" součástí této kružnice (rovnice se musí rovnat-být splněna)
lineárně závislé, to znamená, že nejsou kvadratické? Vím jaký je rozdíl mezi kvadratickým a lineárním členem, avšak nepoznám, jestli je lineárně závislý, nebo nezávislý...
Mohu poprosit o vysvětlení?
2x
Pozor, vše, co jsem psalo dříve, je blbost. Jirka92 má správnou námitku, já jsem se nějak zbláznil či co. Postup tazatelky je špatná od zamého zašátku, rovnice tečny v podobě, ze které zřejmě vychácí, je rovnice tečny , je-li znám bod dotyku a nelze tam dosazovat počátek. takže vše je jinak, snad pomůže to co psal tešna, jinak se k tomu vrátím pořádně. Moc se stydím
doplněno 28.05.15 22:12:Ale i teď jsem se ukvapil, ono to není tak jednoduché. Ve skutečnosti tazatelka počítala dobře, já jsem to teď ex post špatně vyložil. Prosím, neberte mne zatím vážně, já se opravím.
doplněno 28.05.15 23:43:Takže odvolávám, co jsem odvolal, správně je postup tazatelky a všechny mé odpovědí kromě této.
2x
Tak jsem zase tady. A rozebereme si úlohu.
Výchozí objekt je kružnice s rovnicí (po úpravách doplněním na čtverec)
(x+5)² + (y+5)² =1
tedy kružnice o středi [–5, –5] a o poloměru r = 1.
Nyní: Rovnice tečny, jdoucí bodem [x0,y0] je na kružnici (tedy bod [x0,y0] je bodem dotyku) je, jak nás učí teorie,
(*) (x+5)(x0+5) + (y+5)(y0+5) = 1
a tato přímka prochází počátkem. To znamená co? Jednak,dosadíme-li bod [x0,y0] do levé strany této rovnice, dostaneme (x0+5)² + (y0+5)² , a jelikož bod [x0,y0] jako bod dotyku leží na kružnici, je levá strana rovna jedné, čili bod [x0,y0] vyhovuje rovnici (*) a leží tedy na na příslučné přímce (ale to jsme čekali, když je to rovnice tečny). Bod [x0,y0] ovšem neznáme (najít ho je součást zadání), ale požadujeme, aby přímka procházela počátkem, čili aby po dosazení x = 0, y = 0 byla rovnice (*) splněna, Proto tedy elisa ho do této rovnice dosadila a dostala pro bod dotyhu [x0,y0] vztah
5(x0+5) + 5(y0+5) = 1
čili tohle uý není ani rovnice přímky, ani rovnice kružnice, ale vztah pro bod dotyku. Takže její následující postup je v principu správný a možná je správný i numericky. A má první odpověď byla správná,.
Následně při procházce se psem jsem zpaměti zvažoval tu poznámku jirky, jak je možné, že tazatelka má dosazovat bod kružnice a ne pořátek, uvědomil jsem si, že ta rovnice je tečna, pokud [x0,y0] je bod kružnice a tedy za něj nelze dosazovat počátek. Ale to taky nikdo nedělá. Takže odpověď na první Jirkovu otázku je, že bod [x,y] je obecný bod pžímky (tečny) a na kružnici leží bod [x0,y0]. A za ten nikdo nedosazuje, ten počítáme.
děkuji za rozbor, já kdybych použil pořádně hlavu, tak se nikdy neptám, jestli rovnice tečny není i rovnice přímky, mě v tu chvíli nedošlo, že nemůžeme násobit mezi sebou rozdílné členy-x a x0. Rovnice tečny neobsahuje tudíž kvadratický člen
1x
Byl jsem mimo net. Později napíšu víc, teď jen stručně: rovnice tečny je samozřejmě rovnice přímky. V dané úloze hledáme tečnu, jsoucí saným bodem (počátkem) takče tento bod musí rovnici vyhovovat, a hledáme bod dotyku, který tedy musí vyhovovat rovnici tečny i rovnici kružnice. elisa možná zvolila matouci označení x0,y0 pro bod tečny, obecný bod by bylo lébe značit bez těch nulek, ale elisa hledala a označila už ten bod dotyku. Možná i toto je matoucí, pokud se nezorientujete, ještě ze k romu vrátím.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.