Určete povrch a objem rotačního válce, který je vepsán do koule o poloměru r = 5 cm, jestliže se plošný obsah pláště válce rovná součtu obsahů obou jeho podstav.
Poraďte prosím někdo. ![]()
1x
V zadání je : plošný obsah PLÁŠTĚ válce se rovná ...
sečíst dvě podstavy není problém, a výsledek přepočítat na obdélník pláště s jednou stranou rovnající se obvodu té podstavy snad také ne!
Stačí dva vzorce.. Obvod kruhu a obsah kruhu
0x
Úloha je v zásadě opravdu velmi jednoduchá. Dobře radí @hejkal, naproti tomu valec se mýlí. Možná bych nejprve ujasnil pojmy, speciálně válec a pojmy s ním svázané:
Válec je v prostorové geometrii těleso, vymezené dvěma rovnoběžnými podstavami a pláštěm. Plášť je rozvinutelná plocha, všechny povrchové (tvořící) přímky pláště jsou rovnoběžné a pokud jsou k podstavám kolmé, hovoříme o kolmém válci. V opačném případě se jedná o válec kosý. Vzdálenost mezi podstavami se nazývá výška válce. Vzdálenost mezi dvěma podstavami podél pláště (tj. podél povrchové přímky) se nazývástrana válce.
Je-li podstavou kruh, pak válec označíme jako kruhový. Kolmý kruhový válec nazýváme rotačním válcem. Přímku procházející středy obou podstav rotačního válce nazýváme osou rotace.
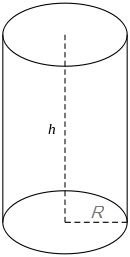
(viz obrázek.)
A k vlastní úloze. Řešení stručně načrtl @hejkal; možná, že až příliš stručně, tak ho přeci jen malimo rozvedu. Při zachování značení z úlohy a z přiloženého obrázku zjevně platí:
1. obsah obou podstav je 2πR²
2. obsah pláště je 2πRh
3.ze zadání jsou tyto obsahy stejné, tedy R = h
4. druhou rovnici pro R a h dá podmínka, že válec je vepsán do koule; Pythagorova věta říká
R² + (½h)² = r²
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.