Dobrý den, neporadil by mi někdo s tímto příkladem?
Jen mi řekně prosím jaký vzorec mám použít. Vím, že by se na otázku dalo odpovědět ,,logicky,, , ale naše učitelka chce mít u všeho vzorce s postupem.
Má to vyjít
3D
4B
5c
Děkuji
doplněno 24.05.15 11:32:Ještě s tímto potřebuji poradit:
F = 400N
y = 0,08 m
k = 5 000 N.m
Jakou práci vyková síla, která prodlouží pružinu ze základní polohy o 6 cm?
Práce se vypočítá W = F* S Když, ale neznám S jak mám dál postupovat?
Děkuji


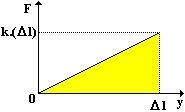
Při natahování pružiny se síla rovnoměrně zvětšuje z 0 na F = kΔl, k je tuhost pružiny, Δl její prodloužení. Práce vykonaná prodloužením je rovna W = ½ kΔl2 = ½ ⋅5000⋅0,062 J (joulů).
Práce je rovna obsahu trojúhelníka v grafu:
Moc Vám děkuji za ty předchozí příklady.
Teď ještě potřebuji poradit s touto úlohou.
add 8 mě vyšlo. Počítal jsem ho podle vzorce T = 1/2pí* (odmocnina l/g)
děkuji

V tomto případě doba kmitu závisí na délce závěsu a tíhovém zrychlení. Na hmotnosti kuličky vůbec nezávisí.
Jestliže se délka zmenší na ¼ , tak odmocnina z ¼ je ½ , takže doba kmitu se zmenší na ½, tj. polovina ze 2 s ... proto odpověď 8C.
Jelikož doba kmitu nezávisí na hmotnosti kuličky, bude odpověď 9B.
Doba kmitu je nepřímo úměrná odmocnině z tíhového zrychlení. Tíhové zrychlení se 4× zmenší, doba se √4 = 2 krát zvětší ... proto 10A
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.
