Ahoj.
Nevěděl by někdo, jak spočítat tenhle příklad? Nemůžu s tím hnout. Díky.
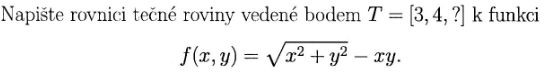
2x
Takže, jak jsem pravil: nejprve dosadím x = 3, y = 4 a vypočtu ? = –7 . Tečná rovina je rovina, jdoucí bodem T = [3,4,–7] a má tedy tvar rovnice
p: z =–7 + A(x–3) + B(y–4)
kde Ah + Bk je totální diferenciál funkce f v bodě [3;4] , tedy vlastně lineární část přírůstku funkce f, vektor (A,B) je její gradient a konstanty A a B jsou parciální derivace.
0x
Moc si toho už nepamatuji, ale funkce přece není prostorová, tak proč tečnou rovinu. Spíš tečnu. A tečnu je dána bodem, ten máme a směrnicí. No a směrnice je první derivace dané funkce.
doplněno 22.05.15 22:46:Sorry asi blbost
Máte pravdu, nemáte pravdu. Ta funkce je funkce dvou proměnných a tedy, chcete.li, prostorová.
doplněno 23.05.15 10:10:No a měli jste vůbec u maturity parciální derivace? Já maturoval ještě o cca deset let dřív a neměli jsme ani ty obyčejné.
To jsem pochopil trochu později že jsou tři proměnné. Zítra 50 let od maturity, no něco si ještě pamatuji. Fakt ale matematikou jsem se neživil. Tu třetí proměnnou myslím levou stranu.
doplněno 25.05.15 22:29:Tak máme po sjezdu. Je nás o 25% méně. Pro zdraví tekla domácí slivovice. Jinak vzpomínám, že ve čtvrťáku již koncem přišly na řadu derivace což má souvislost s limitami. Integrály snad jen základ. Parciální derivace a jednoduché diferenciální rovnice až v prvním či druhém semestru ČVUT. Po čtvrtém jsem to zabalil. Ovšem když jsem zde viděl příklady od studentky prvního ročníku Ekonomie tak jsem žasnul. Za našich časů to snad bylo na 4. semestr.
Když ovšem vidím tu úroveň středoškoláků, tak nevím kolik z nich má šanci jít výše.
No jo, ve čtrtém semstru. aůe na ČVUT a pořádně. Na ekonomce to "zvládnou" komplet za rok letem světem.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.