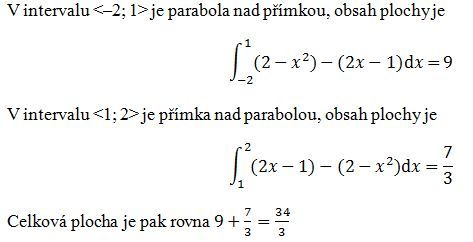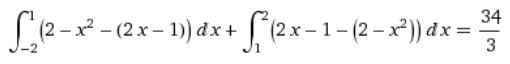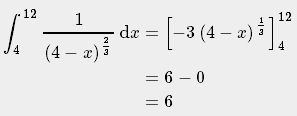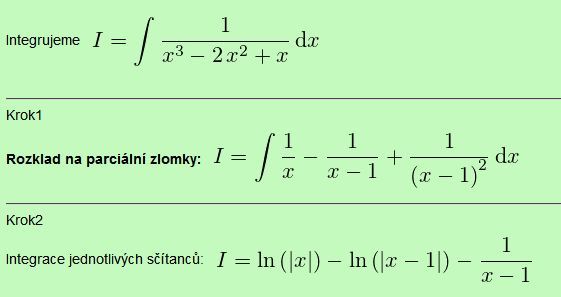Ahoj,
mohl by někdo, vypočítat aspoň nějaký příklad? Potřebovala bych si zkontrolovat výsledky.
Děkuji.
2x
Tak to je příkladů jako máku, opravdu nemáte o žádném ani ponětí? Nebo, pokud máte a máte dokonce výsledky, které chcete jen zkontrolovat, proř je sem nehodíte?
Nicméně se vyjádřím aspoň k něčemu.
Kontrola příkladu 1 se stamdardně provádí zkouškou, to snad zvládnete. Jakkoli příklad sám je pracnější (řešil jste ho Gaussovou metodou, Cramerovým pravidlem, nebo ještě jinak?), zkuška je prosté násobení a sčítání, to prostě musíte zvládnout.
K příkladu 2 jen upozorním, ře derivace arctangenty je 1/(x²+1) a tak integrand po substituci bude y1/3dy, což jistě snadno zintegrujete; zkouška zde spočívá v derivaci výsledku.
Víc zatím radit nebudu. i když bych samozřejmě uměl všechno. Ale projevte aspoň trochu vstřícnosti, a pokud něco nevíte, přiznejte to a napičte, v čem je problém; pokud vám jde opravdu jen o kontrolu, napiište své výsledky.
1x
Tak sem vložte vaše výpočty a my je zkontrolujeme. Např. první příklad počítám pomocí matic. U druhého zavedete jednoduchou substituci a integrál pak již snadno spočtete.

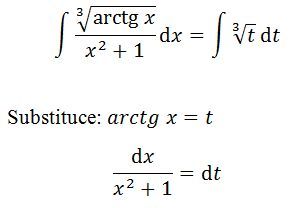
Limitu byste měla dělat u singularity, zde tedy ke čtyřce (tam se "dělí nulou".
Ale podívejte se i na 4. příklad; já se k němu vrátím, ale od pohledu je mi to podezřelé. Například jste nenačrtla graf.
4)
Parabola
f(x)=2-x2
x2=2
x=+-odmocnina2
vrchol y= 2
__________
Přímka
g(x)=2x-1
půjde přes (1,1) , (0,5;0)
__________________
Budu počítat integral:
(mínus) integral od -odmocnina 2 do -2
+ integral od 2 do odmocnina 2
Potom ty dva integrály sečtu
Substituci máte v pořádku, ale u těch křivek a obsahu jste to nepuchopila úplně dobře.
Křívky jste popsala dobře, asi byste je i načrtla. Máte také pravdu, že obsah vypočtete jako ∫(2–x²) dx – ∫(2x–1)dx, ale meze jsou špatně. Musíte spoěítat průsečík obou křivek a vyjdou vám meze x1 = –3, x2 = 1. (někde dříve jste psala, že definiční obor je od minus odmocniny ze dvou do + odmocniny; chyba, definiční oboe obou funkcí je celé R.
No tak tady si nějak nerozumíme. Pokud je definiční obor dán jmenovitě, tak je dán jmenovitě, zadání d.o. má přednost před implicitním ale v tom zadání, které jste napsala původně, nic takového nestojí. A při tom zadání s def, oborem od –2 do 2, tady mi nějak není jasném čím má být přesně počítaná plocha omezená, Mohla byste, prosím, napsat zadání úplně a doslova? Pak se na to podívám, třeba máte pravdu.
doplněno 22.05.15 19:11:A k tomu neurčitému integrálu – nějak mi tam schází druhí mez. Asi napíšu řešení. Ale ne hned.
Tak jsem se k tomu nedostal včas, ale stejně bych nedal tak pěkný obrázek; děkuji.
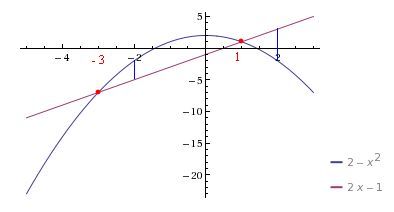
Jen bych to okomentoval s hlediska mých původnívh rad. V zadání, jak bylo napsáno v otázce, jsem neviděl nic o definičním oboru <–2;2> a pochopil jsem to tak, že máme určit obsah obrazce, omezeného grafy funkcí f(x) a g(x). V takovém případě se zadání chápe tak, že grafy funkcí (s definičním oborem implicitně daným jako maximální množina těch x, které lze dosadit, zde tedy u obou funkci jde o celé R) rozdělí rovinu na několik oblastí a máme počítat obsah té omezené. (Kdyby jich bylo omezených více, bylo by třeba upřestnit to v zadání.) V našem případě by to tedy byla oblast mezi průsečíky obou grafů (na obrázku vyznašených červenými body) a integrál bychom brali skutečně v mezích od –3 do +1; přitom fungce g je zde pod funkcí f, takže intefrál ∫fdx bychom přičítali a ∫gdx odčítali.
Děkuji, teď je to jasnější. Podle tohoto zadání to, co jsem k tomu psal, není pravda. Véš výklad bude oravdě blížm ale až zítra vám to zkontroluji a napíšu řešení,
Jen tak pro zají,avost, jakou používáte učebnici? Není to třeba Kaňka ,Coufal, Klůfa, nebo nějaká bovjší?
Není. Za prvé jste se spletla při dosazování; funkce f(x) = F(x, x+1) = xex. Od tohoto okamžiku je vše špatně, a máte tam jeden principiální nedostatek: kfyž do F dosadíte za y, dostanete funkci jedné proměnn= a nemůžete psát f = f(x,y).
Stacionární bod funkce f nicméně vyjde –1, ale bude v něm lokální minimum. (Kvalitativní kontrola, funkce ex je shora neomezená a funkce xex (nebo i 3xex) tím spíš a nemůže tedy jako jediný lokální extrém mít maximum.)
doplněno 23.05.15 13:12:Vlastně by ta chyba neměla hrát roli, protože jste bočítala s trojnásobnou funkcí, která se co do monotonie chová stejně, ale navíc čpatně pracujete s druhou derivací. Podmínka f"/x) = 0 nesouvisí s typem extrému, to je podmínka na inlexní bod (a ten v bodě x = –2 skutečně je). Typ extrému poznáme podle znaménka druhé derivace v tom bodě extrému.
K příkladu 6: uvedla jste podmínky, ještě to chce áčrtek. V podmínkách máte několik chyb:
Podmínka x > y v podě a) je správně, geometricky představuje polorovánu, ležíci pod osou prvého kvadrantu (pod přímkou x = y). Co v tomto bodě znamená to x=y, nevím. Možná je to nějaký mexivýsledek, do řešení to rozhodně nepatří.
Podmínka, uvedená ad b), (tedy x ≠ 2) je v pořádku, geometricky představuje svislici procházející bodem [2;0]. V dalším (v bodě c) zjistíme, že vlastně stačí vyloučit právě jen tento bod.
V bodě c) jste zapoměla, že násobení záporným číslem pbrací smysl nerovnosti, takže podmínka je x² + y² ≤ 4, což geometricky znamená kruch o středu v počádku a o poloměru 2.
Když tyto podmínky spojíme, vidíme, že definiční obor ke půlkruh (o středu v počátku a o poloměru 2) pod osou prvního kvadrandu, s vyloučením bodů této osy (základnového průměru) a bodu [2;0]
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.