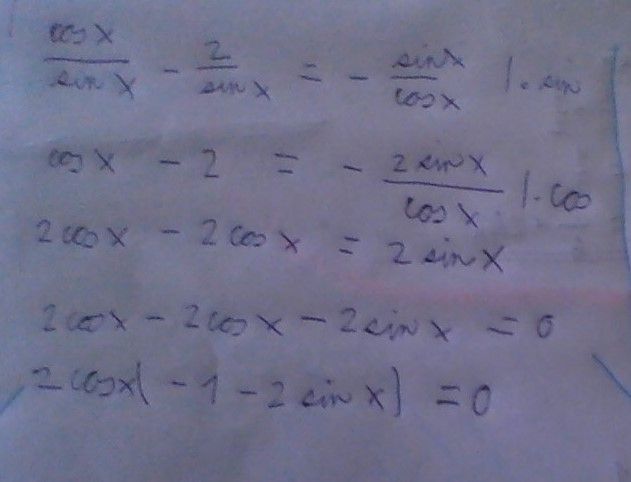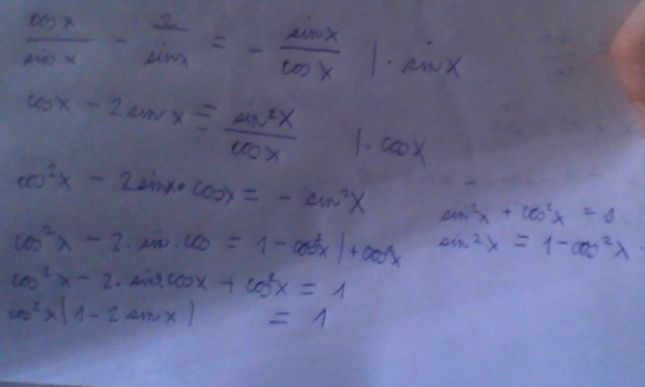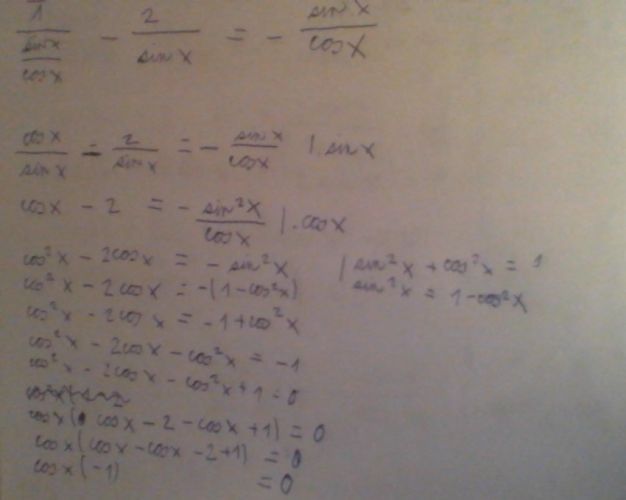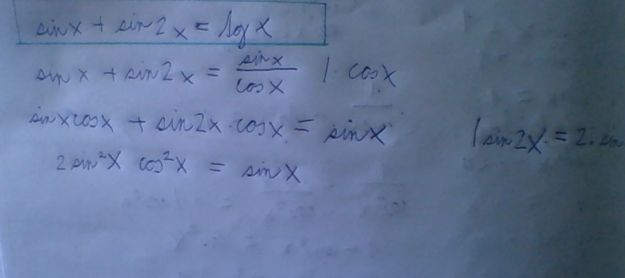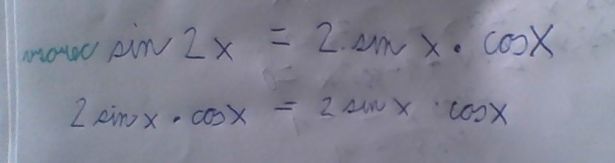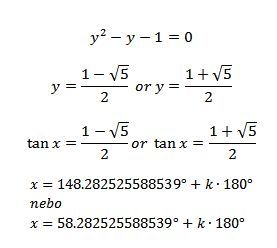Nejste přihlášen/a.
Dobrý den,
neporadil by mi někdo s touto geniometrickou rovnicí? Vůbec si nevím rady. Strašně v těchto rovnicích plavu. Jakým třeba tady použít vzorec?
Nechci aby to vypadalo, že sem hodím jen tak a příklady a vy ho vypočítáte to fakt ne, ale tady si nevím rady ![]()
Velice děkuji za odpověď.
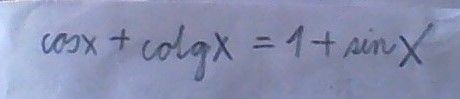
2x
Jistě víte, že tg(x) se dá vyjádřit jako podíl sin(x)/cos(x) a podobně i cotg(x) se dá vyjádřit jako cos(x)/sin(x). Zkuste si to dosadit za váš kotangens ve vzorečku, třeba se s tím pohnete dál.
Asi jsem blbý, ale numím to dosadit. Koukal jsem na netu na vide na toto téma
V tom vydeu to vždy nějak pochopím, ale s tím mým příkladem pořád nevím jak dál.
Jak neumíte dosadit? Prostě si do rovnice místo cotg x napište ono cos x / sin x a pak se zkuste zbavit zlomku.
Stále nic? Tak se na to zkusíme podívat podrobněji. To video je pěkné, ale konkrétně ten váš příklad vám vyřešit nepomůže, ale to nevadí, on je totiž mnohem jednodušší.
Takže, rovnice je
cos x + cotg x = 1 + sin x
a doporučený vzoreček
cotg x = (cos x)/(sin x)
ty závorky jsou možná zbytečné, ale předejdeme jimi nejasnostem – snad. Dosadíme do rovnice, to jest, místo kotangenty napíšeme její vyjádření ze vzorečku:
cos x +(cos x)/(sin x) = 1 + sin x
Teď máme rovnici se zlomkem, ve vyjádření kotangenty je zlomek, který má v čitateli kosinus a ve jmenovateli sinus. Jak se z rovnice odstraňují zlomky? Nu, rovnici společným jmenovatelem všech zlomků vynásobíme; tady je jediný zlomek, tedy také jediný jmenovatel. (Jen na okraj: od tohoto okamžiku až k samotnému závěru můžete na goniometrické funkce zapomenout a místo sinu x si představovat třeba A a místo kosínu Ň.) Po vynásobení sinem – což je ten společný jmenovatel – dostaneme
(cos x)*(sin x) + cos x = (1 + sin x)*sin x
po vytčení kosinu z levé strany rovnice
(cos x )*(sin x + 1) = (1 + sin x)*sin x
čili
(cos x )*(1 +sin x) = (1 + sin x)*sin x
a po zkrácení
cos x = sin x
Když nyní vydělíte rovnici kosinem (podmínka: cos x ≠ 0) dostaneme
tg x = 1
a to už opravdu nechám na vás. (To jsme v tom závěru, takže si zase vzpomeneme, že počítáme s goniometrickými funkcemi.)
Jak jednoduché. Tak jsem si v noci počítal, pravou stranu roznásobil a pak slepě nevidím zkrácení. Hned bych do toho zatáhl sinus 2x. Špatná cesta.
Velice Vám děkuji Kartáginec.
Zkoušel jsem počítat další příklady, ale pořád se v tom motám. Tento příklad jsem počítal dle vzorce cosx2+sinx2=1.
Bohužel nevím jak mám v tomto příkladu dál postupovat. Neporadil by jste mi ještě?
Děkuji
doplněno 07.05.15 21:49:Dále tomůžu sečíst : -2sin2x+sinx + 1 = 0
Ted vznikla kvadratická rovnice, takže použiji diskriminant D= b2-4ac ;x = (-b odmocniaD)/2a
Vím, že to zní blbě, ale jak mám siny dát do diskriminantu? Můžu si říct -22y+1y + 1= 0?
D= 1-4(-2).1
D= 9
D= odmocnina 3
X1= -1 +3/-4 = -0,5
X2=-1-3/4= 1
To je vše? Kdybych měl zde dělat podmínky tak ty zde budou jaké?
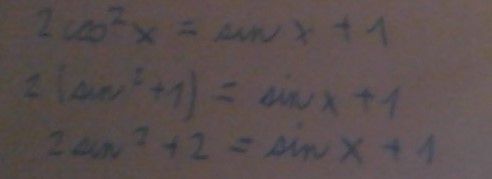
Nevím zda postup povede k výsledku, ale copak nevidíš tu hrubou chybu vyjádření cosinu sinem
doplněno 07.05.15 22:55:Jednoduché, postup je správný, nedělej chyby. Malá nápověda vzorec a²-b² a výsledek sin x = 0,5
doplněno 07.05.15 23:07: Tahle úprava je sice špatně -2sin2x+sinx + 1 = 0ale řeší se to substituci sin x = p-2p² + p + 1 = 0doplněno 07.05.15 23:09:
Nějak se to slilo sin x = p zbytek je kvadratická rovnice
Pokud ty 3 řádky v obrázku je postup výpočtu tak snad cos² x = 1 - sin² x
doplněno 08.05.15 12:21: Pokud je poslední řádek obrázku 2sin² + 2 = sin x + 1 tak úprava -2y²+1y + 1= 0 je taky špatně. S takovými školáckými chybami se nikam nnedostanešdoplněno 08.05.15 12:39:
Sorry doplněk před tímto beru zpět
Kontrolovat to nebudu. Zkusím to jinak
2 cos² x = sin x + 1
2 (1 - sin² x) = sin x + 1
2 (1 - sin x) (1 + sin x) = sin x + 1
2 (1 - sin x) = 1
1 - sin x = 0,5
sin x = 0,5
doplněno 08.05.15 13:36:Měl bych doplnit podmínku že
sin x <> - 1 což je ale druhý kořen kvadratické rovnice
Nepíšu o výpočtu ale doplněk 7.5 21.49
doplněno 08.05.15 13:24:Jinak v tom zápisu výpočtu že D je odmocnina ze tří je děs. Byť dále je to správně
doplněno 08.05.15 13:29:A snad ti vyšel sin x = 0,5 jako jeden z kořenů kvadratické rovnice
Ano už to vidím, to jsem zapsal jako pí/6.
Teď další příklad - předem děkuji za trpělivost ![]()
tgx jsem zde nahradil na sinx/cosx .
Jak mám, ale dál postupovat v tom 3. řádku? Nejdřív přece musím sloučit nějak zlomky nalevo. Odečíst to nejde, takže mám použitím substituci a nahradit cos?

Kontroluj si po sobě. Že nepíšeš x budiž, ale třetí řádek, první zlomek, jmenovatel je špatně
doplněno 08.05.15 14:11:Obě strany vynásobíme sin x cos x, mocninu sin převedeme na cos a mělo by vyjít cos x = 0,5
doplněno 08.05.15 14:16:A stanovit podmínky
tg x <> 0 to snad ani nemůže být
sin x <> 0
Už ti musím napsat, nepi. Co v druhém řádku, v druhém členu dělá ten sinus
doplněno 08.05.15 20:24:A že ti ve stejném řádku na pravé straně chybí mínus
doplněno 08.05.15 20:28:To minus tam je napatlané, ve třetím řádku se s ním počítá
Je to pro mne nečitelné. Přece šestý řádek vykrátit na obou stranách cos² x a zbude
-2 cos x = - 1 / - 2 to za lomítkem je výraz vydělit
cos x = 0,5
doplněno 08.05.15 21:42:Co to je za úpravu pod tím škrtlým řádkem. To snad vytýkáš cos.
Vždyť se to cos² x vyruší
Ano vyšlo to!
Fakt moc děkuji za Vaši trpělivost.
Další příklad je tento. Je možné, že to vyjde 0? Cos = 0; cos=pí/2
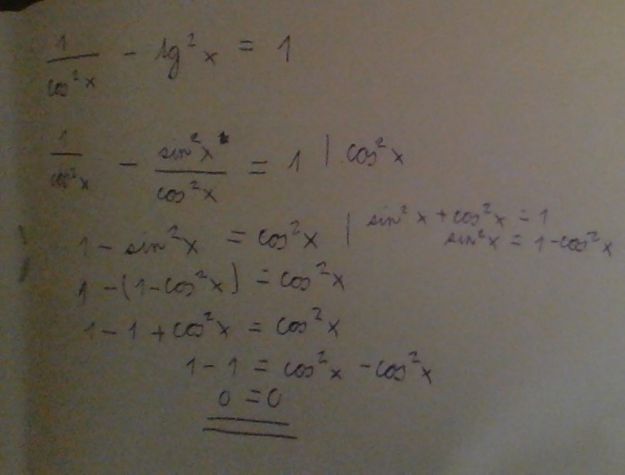
Špatný závěr. Došel jsi k tomu, že 0=0 což je pravda
Stačilo jen ve třetím řádku převést sin na druhou stranu rovnice a musí ti byt jasné, že tento výraz platí pro jakékoliv x
Závěr rovnice má nekonečno řešení
doplněno 08.05.15 22:10:Ovšem podmínka že cos x <> 0
Nevím co bych si bez Vás dneska počal.
Zkouším tento příklad. Ta dvojka v kruhu není mocnina.
Jak mám postupovat dál? Res. co mám udělat s tou dvojkou?
doplněno 08.05.15 22:20:
Vložil jsem špatný obrázek. Omlouvám se. Správně má být ten druhý.
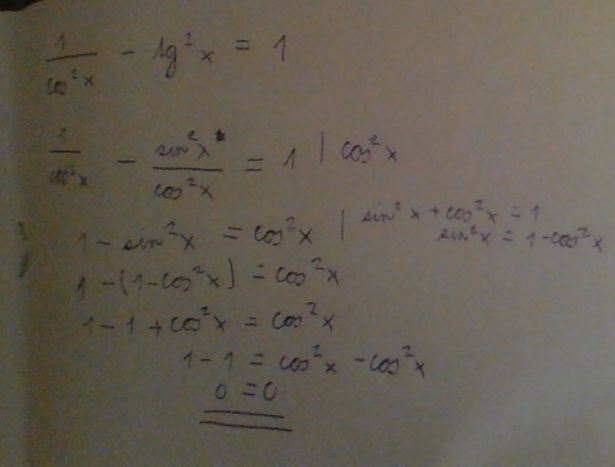
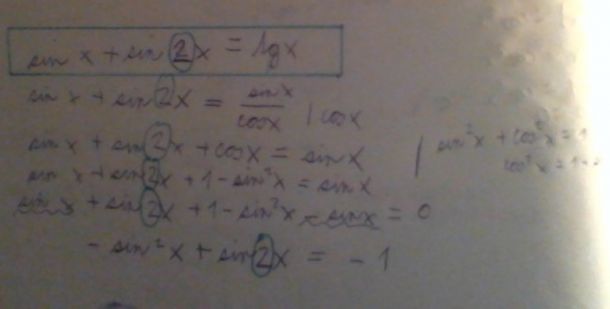
Mrknu a nepomohl by základní vzorec
sin 2x = 2 * sin x * cos x
doplněno 08.05.15 23:27:Měl by pomoci
Dosadíme,obě strany rovnice vydělíme sin x a pak obě strany vynásobíme cos x
Dostaneme 2 cos² x + cos x - 1 = 0
Substituce p = cos x a vyřešit kvadratickou rovnici
Ta sebe kritika sedí. Do toho vzorce se nedosahuje. Sin 2x se nahradí pravou stranou toho vzorce
Stejně jako tg x nahrazujeme podilem
doplněno 09.05.15 11:06:Základní goniometrické funkce třeba tady
doplněno 09.05.15 11:16:Dobře měl jsem použít slovo sin 2x nahradíme, pak obě strany vydělíme sin, následně obě strany vynásobíme cos, provedeme substituci a řešíme kvadratickou rovnici
To jsou snad obě strany stejné. Nahrazeno, další postup popsán, to dělení sin je násobení prevracenou hodnotou, takže krát (1/sin x)
(sin x) + (2 * sin x * cos x) = (sin x/cos x)
Tamten příklad už mi vyšel. Chyba byla v tom dosazování jak jste psal.
Teď počítám tento příklad.
tgx - cotgx = 1
Myslím, že se mi povedl dobře. Jen nevím jak mám zapsat kvadrnty
sin x = 1 (1+2 kvadrant) 1 kvadrant je pí/2, ale jak bude ten druhý?
_______________________________________________________
sinx = -1/2 (3+4kvadrant) Jak mám tyto zapsat, když v tabulkách není sin -1/2?

Asi jsem měl kontrolovat. Těžko bude počítat goniometrické rovnice, když výpočty trpí takovými základními nedostatky jako sin x * sin x = 2 sin x, případně úprava rovnice atd.
Děkuji za opravu.
Přiznávám, že mám s goniometríí velké mezery, ale oproti prvnímu dotazu v této sekci jsem se trochu zlepšil. Bohužel jsem počítal ještě tento, poslední příklad, který mě nevyšel.
Prosím, vás naposledy, co jsem zase udělal špatně?
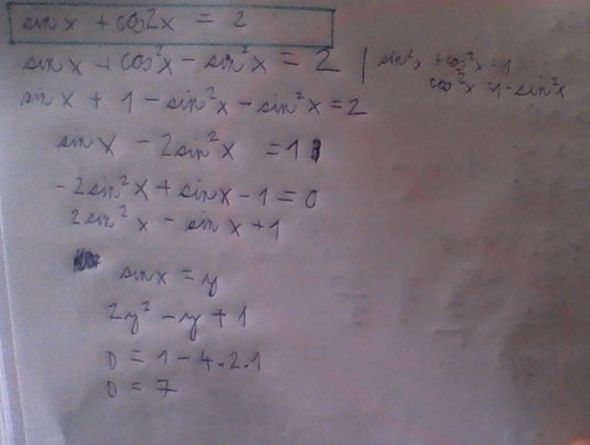
Nejde o goniometrické, děláš základní chyby. Až po tu kvadratickou rovnici chybu nevidím
doplněno 09.05.15 19:38:Teď koukám že diskriminat je záporný, rovnice nemá řešení v oboru reálných čísel
Teď již poslední otázka. Na bych měl u toho příkladu zapsat podmínky existence? Když mám zlomek tak podmínky umím zapsat, ale tady to je jak?
Omlouvám se, že zase otravuji.
U tohoto příkladu nerozumím tomu konci. Ted bych měl dosadit do diskriminantu. Když tak, ale učiním výjde mi číslo 5 to je dobře?
Děkuji

Je to dobře a není to nic proti ničemu. Dizkriminant je kladný, čili kvadratická rovnice má dvě reálná řešení, a protože tangenta má jako obor hodnot celé R, obě jsou pouřitelná. Pro x (tedy pro argument tangenty) dostaneme dvě základní řešení, která leří v intervalu (– ½π, ½π) a nekonečně mnoho dalších,když k těm dvěma přičteme celé násobky pí.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.