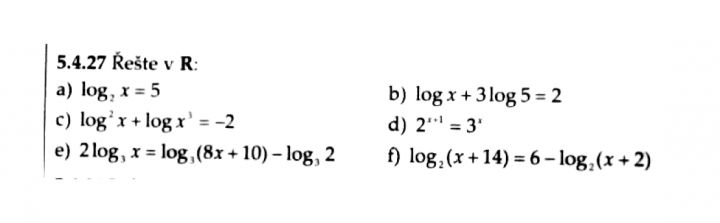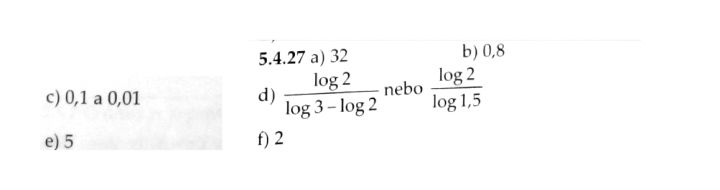Zdravím. 2^x+1=3^x. Neví někdo, co s tím? Když to zlogaritmuji, nevychází mi z toho nic kloudného. Díky!
0x
doplněno 03.05.15 19:28:
Pardon, 2^(x+1) = 3^x , jak je ostatně vidět na přiloženém obrázku.
Jasně, rozumim tomu ohledně jirakzxc. Ale závěr méhoříkladu je, že jej snadno vyřeším a vyjde mi to, co panu Hruškovi? To bych sem přece nepsal,kdybych věděl, jak to vvyřešit...Mám pouze výsledek, ale jak se k němu dojde mi pořád uniká ![]()
Anebo přímo zlogaritmovat. Prostč správné zadání je triviálně řešitelníá. Omlouvám se tazateli, ale vy jste tvrdil, že si neumíte poradit s tím špatným zadáním, domníval jsem se, že správné zadání vám potíže už dělat nebude.
0x
Stále si myslím, že původ problému vychází z nedorozumnění. Je ale fakt, že má první odpověď byla poněkud znehodnocena typograficky, a navíc původně obsahovala překlep, i když jsem ho opravil. A protože z vašich odpovědí mi není jasné, že jsme si vše vyjasnili (možná ano, nevím), shrnu řešení úplně a přehledně.
1. Úloha, tak jak jste ji uvedl, zněla:
Řešte rovnici2^x +1 = 3^x
Abych vyloučil nedorozumění, zapíšu uvedenou rovnici ještě dvěma jinýmy způsoby.
Jednak s nadbytečnými, ale upřesňujícími závorkami:
(2^x) +1 = 3^x
a jednak pomocí horního indexu:
2x+1 = 3x.
K tomuto zadání jste napsal – a já s tím souhlasím – " Když to zlogaritmuji, nevychází mi z toho nic kloudného."
Později jste uvedl řešení z výsledků ze zdroje:
Zdroj: státní maturita z matematiky v testových úlohách vč.testových řešení. Miroslav hruška, totiž x = log2/log1,52.
Jedno řešení nalezl jirkazcx, totiž x = 1. Postupovel tak, že řešení uhádl a výpočtem ověřil. Toto řešení ovšem není to, které uvádí Hruška a kolektiv. Je možné, že existuje ještě jié řešení?
3. Jednoznačnost řešení x = 1 dokážeme úvahami o monotonii výrazu (3^x – 2^x). Jak? takto:
Pro x kladné je 3^x> 2^x, pro x = 0 je (3^x – 2^x) = 0, takže řešení rovnice (3^x – 2^x) = 1 může nastat pro jediné nezáporné x, totiž pro x = 1.
Pro x záporné naproti tomu je (3^x – 2^x) záporné a rovněž se nemůže rovnat jedné.
Závěr: Vámi uvedené rovnice má jediné řešení, totiž x = 1 ≠ log2/log1,5.Ke správnému řešení se vrátím v násleující odpovědi.
Správné řešení spočívá v odstranění nedorozumění.
4. Zadání, tak jak ho uvádí Hruška, zní
2^(x+1) = 3^x
nebo, pomocí horního indexu,
2x+1 = 3x,
Zlogaritmujete-li toto zadání, už není pravda, že nedostanete nic kloudného, naopak, tato cesta vede přímo k výsledku. Proto jsem napsal,
"v citovaném zdroji se jedná o příklad
2^(x+1) = 3^x,
který jistě snadno vyřešíte a vyjde vám to, co panu Hruškovi."
(tohle je již po opravě překlepu), ale možná díky překlepu, možná díky tomu, že se mi text "zdrcnul", jste si nevšiml, že jde o jiný příklad, než na který jste se ptal, protože tohle opravdu jistě umíte.
5. Jedno řešení napsal @x.
6. Druhé řešení, která odpovítá tomu, když rovnici zlogaritmujete, je
(x+1) log 2 = x log 3
x(log 2 – log 3) = log 2
x = log 2 /(log 2 – log 3) = log 2 / log ½ 3
7. Uvítám, když napíšete, zda je vám vše jasné.
Jak z toho pozoruji tak někteří neználci nezvládnou ani pořádný jednoznačný zápis. Já tam viděl absolutní člen
Stačily jen dvě závorky
Logickou úvahou jste zjistil, že x nemůže být 0 ani záporné ale pak jste to x stejně uhodl, co kdyby byla rovnice:
3^x - 2^x =1234
To už by nešlo tak snadno uhádnout, protože to pravděpodobně není ani celé číslo.
Dokonce jsem ho ani neuhodl já, to řešení vymyslel jirkazxc. (Navíc posloupnost je jiná: nejdřív jsme řešení uhádli a pak jsme dokázali jeho jednoznačnost, ale to je jen technický detail.) A proč mi to říkáte, já to přece vím. Nebo to byl dotaz?
Ona totiž je to transcendentní rovnice, kterou neumíme řešit v radikálech nebo tak nějak "rozumě", Na to jsou přibližné metody, které rovnici vyřeší s libovolnou přesností. (Zde by vyšlo x ≈ 6,54552.) Analyticky lze dokázat zase jenom jednoznačnost, podobně jako v naší rovnici. (Mimochodem to je důvod, proč se mi to zadání od počátku moc nezdálo jako příklad k maturitě, i když jsem to nijak nerozváděl.)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.