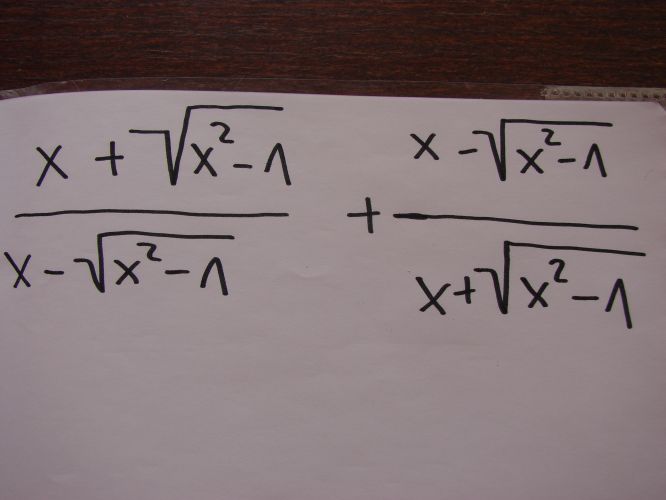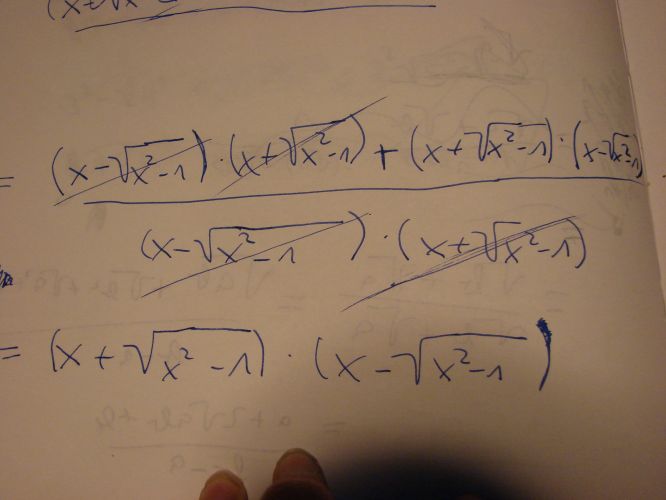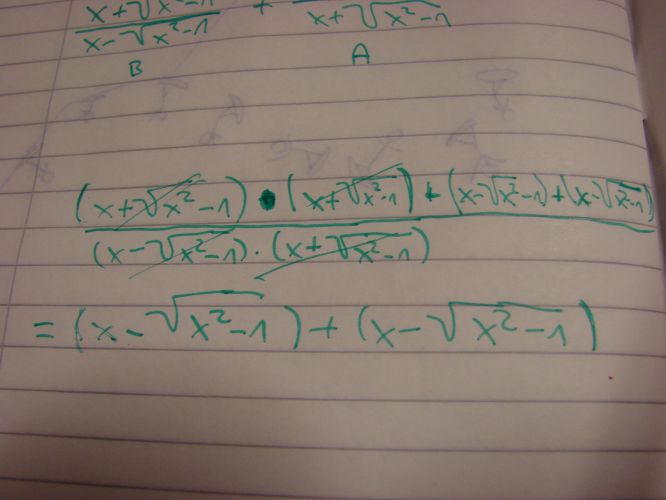Dobrý den, můžete mi nějak pomoci s tímto příkladem? Vůbec nevím co s tím. Moc děkuju.
Nejdřív bych si ujasnil pojmy. Tohle není žádné rovnice, kterou bychom mohli řečit, ale výraz, který zřejmě máte upravit.
A co myslíte tím "Takže to bude..."? To rozhodně není převedení na společného jmenovatele. to, co jste napsal/a, je ten společný jmenovatel. A co dál? Dokončit ten převod, čili upravit ještě oba čitatele a násoledně roznásobit, co je vhodné. Nepřipomíná vám společný jmenovatel nějaký vzoreček? Měl by, ale pokud ne, nevadí, prostě to otrocky roznásobte a vyjde to taky, i když postup bude trochu delší.
A, last but not least, nezapomeňte na podmínkly.
1x
Vidíte, že pod odmocninou je stále stejný výraz a také ze jednou máte "x + odmocnina" a podruhé "x - odmocnina". Zkuste si to zjednodušit tak, že si řeknete, že "x + odmocnina" je třeba A a "x - odmocnina" je třeba B.
Takže s touto substitucí (nahrazením) bude váš příklad zjednodušeně vypadat A/B + B/A, takže po převedení na společného jmenovatele A.B budete mít A.B + B.A a to celé lomeno A.B a pak se pokračuje dál...
Možná se mýlím, tohle jsem celý život nepotřeboval jenom vyhrabuju zbytky tohoto počítání ze zasunutých koutků paměti. Děti zvyklé na příklady z Bělouna to jistě už mají spočítané a správně.
Nemyslím, že byste se mýlil v řešení, měl jsem na mysli váš odhad schopností tazatele (... to asi umíte...)
uf, to mi padl kámen ze srdce, už jsem se zastyděl, že to řeším špatně...
Jen chci, podobně jako Vy, tazatele trošku trknout, aby se sám chytil pak měl radost z toho, že s malou nápomocí najde správné řešení a podle toho se naučí řešit i jiné podobné školní úlohy
No jo no, ne každý má matematické myšlení, můžete se podívat zatím na to, co jsem spočítala, jestli je to správně a poradit jak se to dělá dál? Děkuju mockrát. 
Omlouvám se, drobný přepis tam přeci máte, já reagoval na to předchozí. V čitateli bude A*A + B+B; tp je zíéroveň odpověď na otázku zadavatele: není to dobře.
teď koukám, jakou blbost jsem tam narychlo plácnul, kartaginec to napsal správně A.A + B.B to celé lomeno A.B, omlouvám se
Kartaginec tohle sice napsal správně, ale zato neprávem sepsul "blbost". Tyhle pozdní noční hodiny nejsou nic moc.
Vždyť to je blbě vykráceno
Čítatel vzorec (a+b) ² = a²+2ab+b²
Jmenovatel (a+b) (a-b) =(a²-b²)
Takže Čítatel = 4x²-2
Jmenovatel =1
Vy jste to neroznásobil.
Ale snažite se, zkusím to tedy vysvětlit podrobněji. Použiji označení které navrhl host, a vaěeho označení odmocninýy, tedy
x + "odmocnina"(x² –1) = A
x – "odmocnina"(x² –1) = B
a ještě k pozdějšímu použití označím
"odmocnina"(x² –1) = c
Takže zadání je, upravte výraz
A/B + B/A
Zašneme převodem na společného jmenovatele. Jak jste správně uvedl, společný jmenovatel bude A*B. Převod pak spočívá v tomto: Upravíme jednotlivé zlomky rozšíření tak, aby v jejich jmenovateli bylo totéž, tedy
A/B = (A*A)/(A*B), B/A =(B*B)/(A*B) a sečteme:
A/B + B/A = [(A*A)+B*B)]/(A*B) = (A² + B²)/(A*B).
Teď zbývá upravit čitatele a jmenovatele. Doporučoval jsem začít úpravou jmenovatele. Napíšeme ho jako (1 +c)(1–c) a použijeme vzoreček pro rozdíl čtverců. Zkuste to, prozradím, že vyjde 1. No a výrazy v šitateli uoravte podle vzorce pro druhou mocninu součtu respektive rozdílu, a ono se to zase zjednoduší. Zkuste to, snad už to půjde, a když ne, tak se zase ozvěte.
Jak koukám, hodně napověděl i "blbost" (ale taky tam má chybu).
doplněno 15.04.15 09:32: Musím se opravit (bylo už moc pozdě). Ten jmenovatel samozřejmě nenapíšeme (1 +c)(1–c), ale (x +c)(x–c)S tím (tedy s psaním A = (1 +c) , B = (1–c) místo správného zápisu) souvisí i má výtka "blbost"i. samozřejmě to má správně.Takže znovu . Jmenovatel je (x +c)(x–c) = x² –c² = x² – (x² – 1) = 1 , Čitatel: A² +B² = (x +c)² + (x–c)² = (x² +2xc +c²) + (x² –2xc +c²) = 2 (x² +c²) = 4 x² –2A ještě snad rozvedu tu poznámku, že je to blbě zkráceno: ono primárně je to blbě napsáno, a s tím krácemním je to tak, že nemůýete krátit jmenovatel proti kusu čitatele (a to není jediná chyba, ale to je ta základní).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.